【数据物语系列】 漫谈数据分布可视化分析

Posted on | In |
Words count in article: 4.5k 字 | Reading time ≈ 17 分钟

在实际工作中，我们经常会遇到一堆数据，对数据的有效分析至为关键，而数据的分布就是一种非常重要的数据属性，需要通过合适的可视化手段进行分析。

FesianXu 20221125 at Baidu Search Team

前言

在实际工作中，我们经常会遇到一堆数据，对数据的有效分析至为关键，而数据的分布就是一种非常重要的数据属性，需要通过合适的可视化手段进行分析。本文参考[1]，基于seaborn库介绍一些常用的数据分布可视化方法。如有谬误请联系指出，本文遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明并且联系笔者，谢谢 。

联系方式：

e-mail: FesianXu@gmail.com

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

公众号：机器学习杂货铺3号店

数据的分布，我们可以理解为是“数据的形状”。一个“完美”的数据分布，会将数据所有可能的数据点都囊括其中，因此数据的分布表征了不同数据之间的本质区别。然而现实生活的数据不可能对所有可能的数据点都进行遍历（因为通常会有无限个数据点），因此我们通常都是在某个采样的子集中，尝试对数据本原的分布进行分析。常见的数据分布可视化方法有以下几种：

  1. 直方图（Histogram）
  2. 条件直方图（Conditional Histogram）
  3. 核密度估计图（Kernel Density Estimation，KDE）
  4. 累积分布函数图（Empirical Cumulative Distribution Function， ECDF）
  5. 箱型图（boxplot）
  6. 提琴图（violin plot）
  7. 二元直方图（bivariate histogram）
  8. 联合概率分布曲线（Joint Distribution Plot）
  9. 边缘概率分布曲线（Marginal Distribution Plot）

如Fig 1.所示，我们以penguins数据集为例子分别进行介绍。

Fig 1. penguins数据集，一共有344条数据，每条数据有7个维度的属性。

单变量直方图

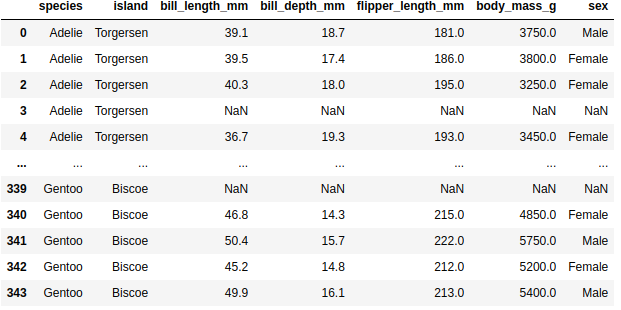
单变量直方图（univariate histogram）是一种单变量的分布可视化方法，将所有数据点进行分桶，然后统计落在某个桶里的数据点的频次，以柱形图的形式将每个桶的频次绘制出来。如Fig 1.1所示，我们对penguins数据中的flipper_length_mm属性进行直方图绘制。

1
2
3
4
5
6
import seaborn as sns
data = sns.load_dataset("penguins", data_home="./data/seaborn-data")
# 可以挑选不同的分桶数量bins，或者每个桶的宽度
ret = sns.displot(data, x='flipper_length_mm', bins=20)
ret = sns.displot(data, x='flipper_length_mm', bins=50)
ret = sns.displot(data, x='flipper_length_mm', binwidth=5)

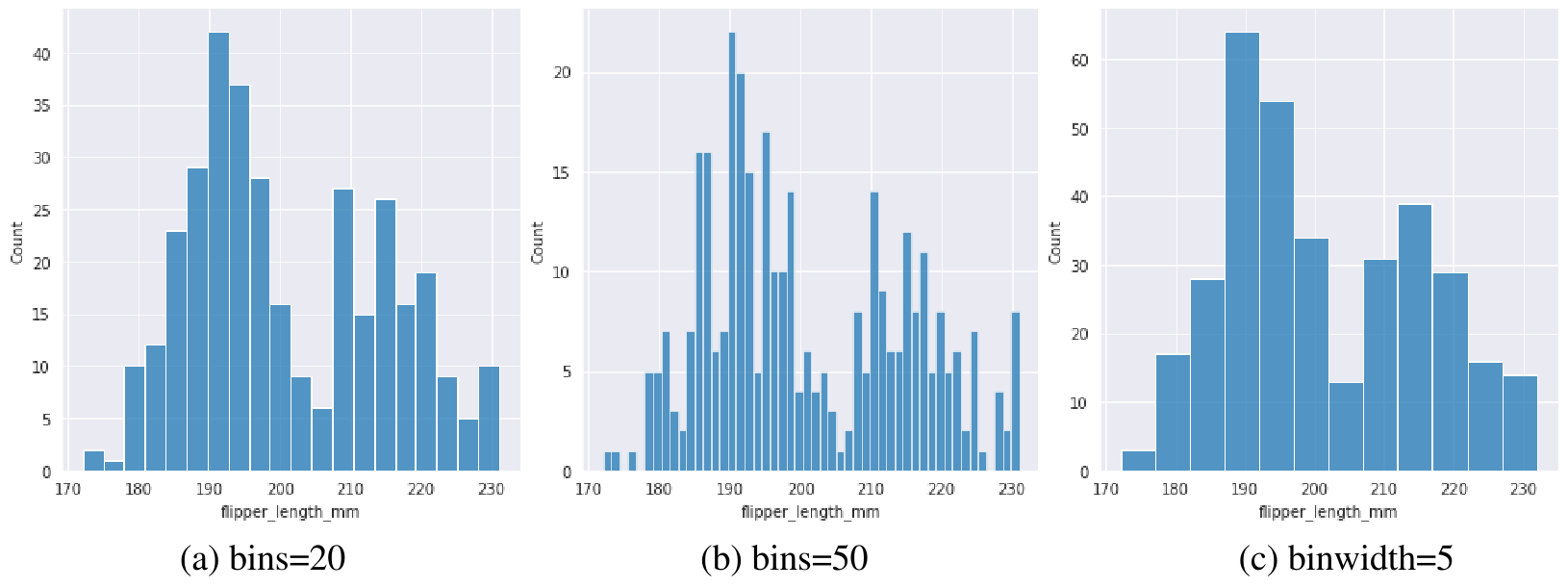
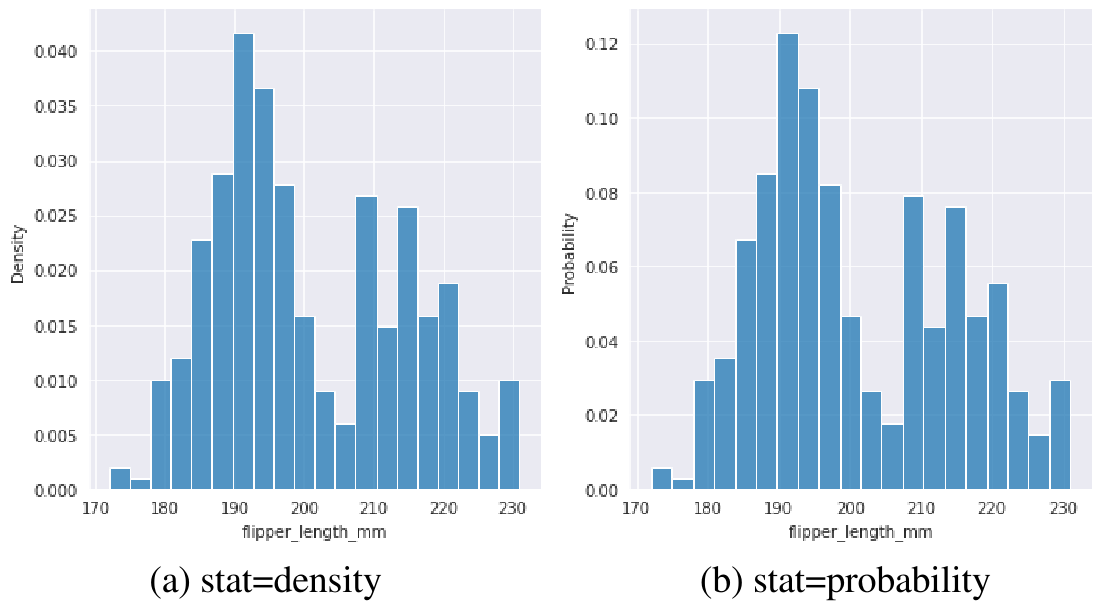
Fig 1.1 对penguins数据的`flipper_length_mm`属性进行绘制直方图，从左到右，分别是（a）分桶数是20，（b）分桶数50，（c）分桶宽度是5。

我们发现，选取不同的分桶数量和分桶宽度对于整个分布可视化结果影响很大。分桶越多，分布越细致，但也越容易被某些噪声影响我们分析整体分布趋势，一般在实际中我们通常会选取多个分桶数进行尝试。原始的直方图统计的是分桶中的数据频次，不同数据的总数不同因此频次并不可比，通常可以考虑进行归一化处理。如Fig 1.2所示，通常有两种类型的归一化：密度归一化，概率归一化。密度归一化指的是所有柱形面积和为1，概率归一化指的是所有柱形的高度和为1。密度归一化的情况下，由于纵坐标的数值会受到横坐标数值尺度的影响，通常是不可比，而概率归一化不需要考虑横坐标的数值尺度，因此通常是可比的。

1
2
ret = sns.displot(data, x='flipper_length_mm', bins=20, stat='density') # 密度归一形式的归一化
ret = sns.displot(data, x='flipper_length_mm', bins=20, stat='probability') # 概率归一形式的归一化

Fig 1.2 （a） 密度归一形式的归一化； （b）概率归一形式的归一化。

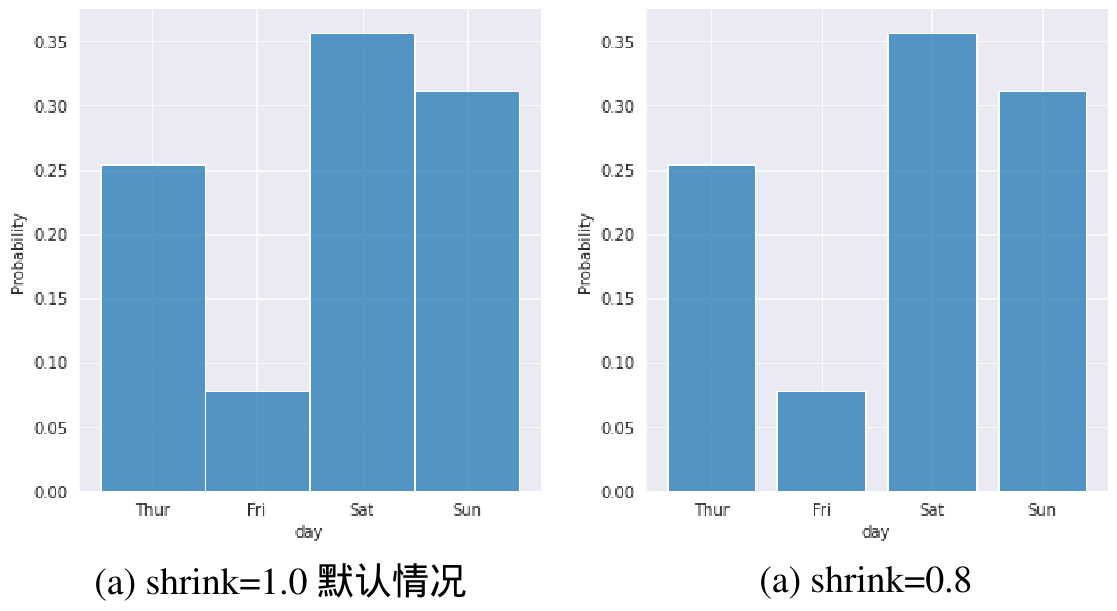
我们既可以对连续变量进行直方图统计，也可以对离散变量进行直方图统计，如Fig 1.3所示，我们通过设置shrink参数，可以控制柱形的宽度，使得可视化效果更像是一个离散变量的直方图。

1
2
3
tips = sns.load_dataset('tips')
ret = sns.displot(tips, x='day', stat='probability')
ret = sns.displot(tips, x='day', stat='probability', shrink=.8)

Fig 1.3 （a）shrink=1.0的情况，柱形之间“肩靠肩”，没有间隙；（b）通过设置shrink=0.8，可以使得离散变量的柱形之间存在间隔，看起来更“离散”一些，与连续变量直方图有所区别。

条件直方图

再回到Fig 1.2，我们能明显地发现这个分布有明显的两个峰，这个flipper_length_mm代表的是企鹅的鳍肢的长度，这个属性会受到其他什么属性的影响呢？在之前的直方图中，我们绘制的是概率分布，如今我们需要绘制条件概率分布，以考察到底是其他哪些属性影响了企鹅的鳍肢的长度。如Fig 2.1所示，由于笔者觉得种类，性别，和居住的岛屿可能会影响到企鹅的鳍肢长度，我绘制了，，的几种条件分布。从Fig 2.1（a）可以发现企鹅的种类的确有所影响（Adelie种类和Gentoo种类的企鹅的鳍肢分布显著不同），而雌性雄性企鹅的鳍肢长度都呈现双峰分布，因此并不是导致Fig 1.2中出现双峰分布的原因，同理，从Fig 2.1（c）中可以发现企鹅居住的岛屿也是导致出现双峰的原因。这些条件分布都可以通过设置displot()中的hue参数实现。

1
2
3
ret = sns.displot(data, x="flipper_length_mm", hue='species')
ret = sns.displot(data, x="flipper_length_mm", hue='sex')
ret = sns.displot(data, x="flipper_length_mm", hue='island')

Fig 2.1 （a）-（c）是不同的条件分布直方图。

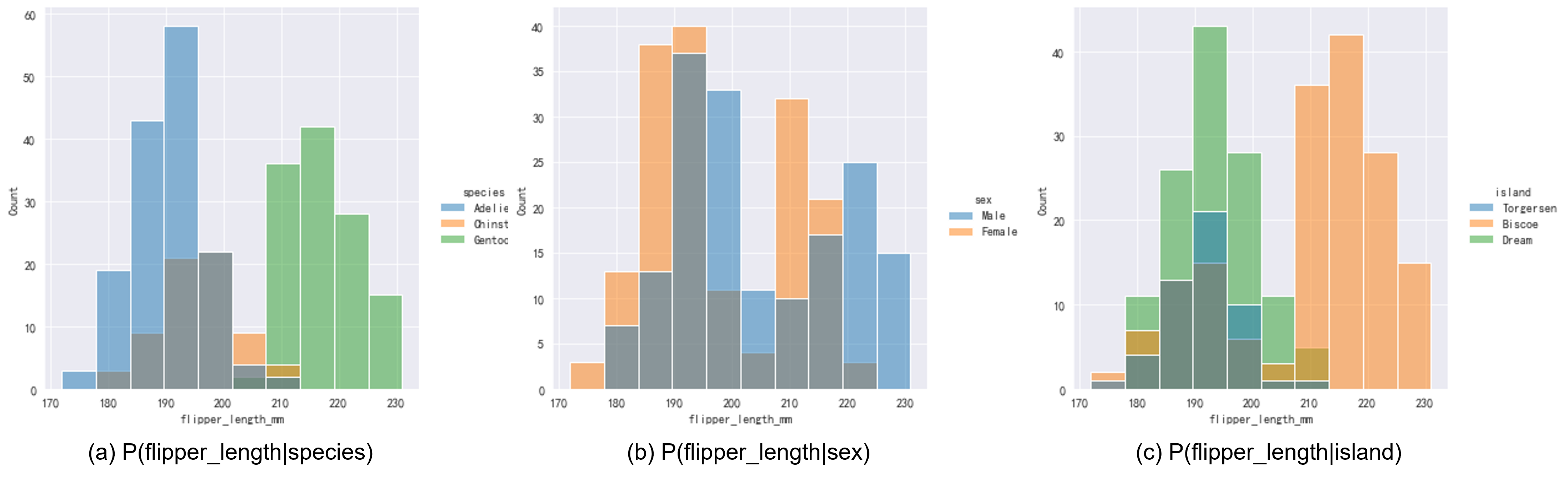
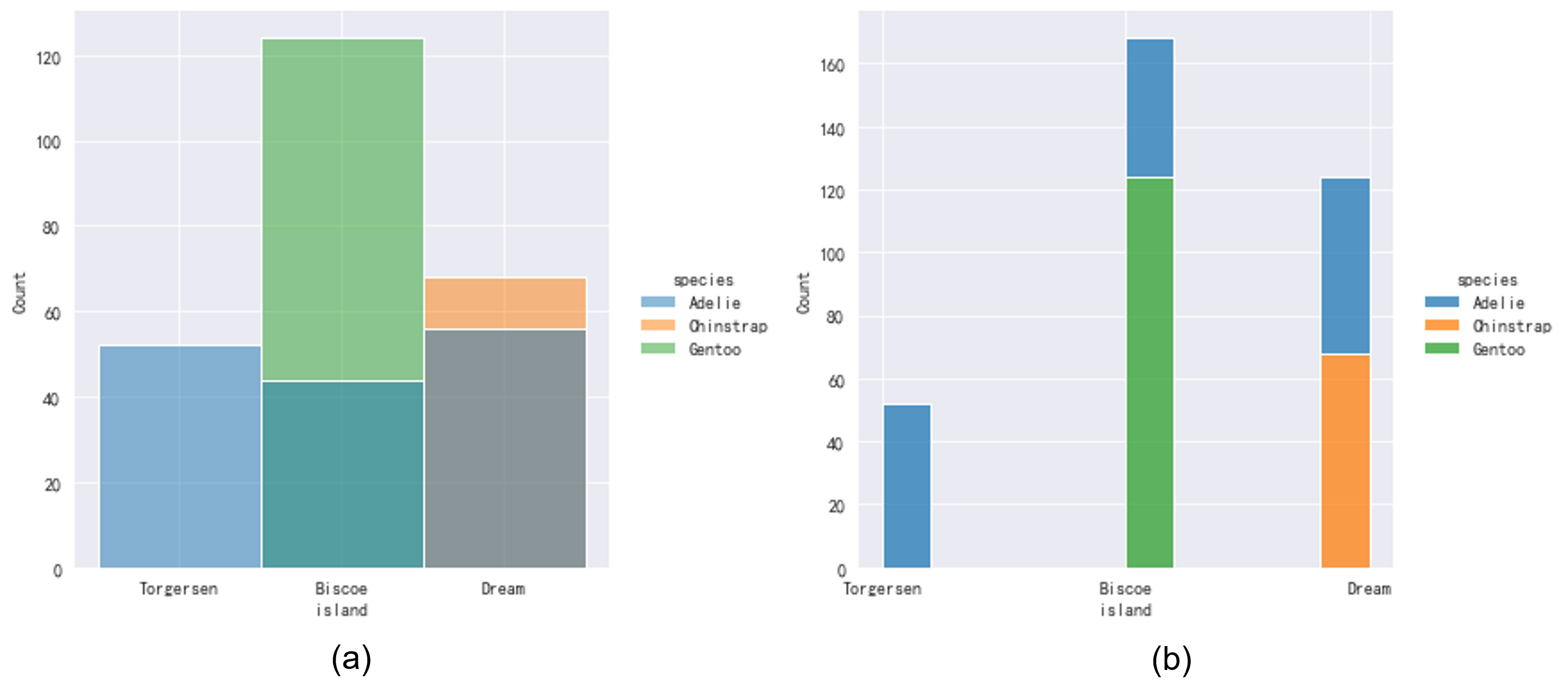
但是居住地会影响企鹅的鳍肢生长发育，这一点比较奇怪，可能并不是一个直接原因，也许是不同岛屿居住的企鹅种类不同导致的？我们可以绘制条件分布进行考察，如Fig 2.2所示，其中的（a）是一般形式的条件分布柱形图，我们发现不同条件下的柱形会存在层叠，容易看不清楚，此时可以通过设置multiple="stack"将其设置为stack模式，柱形图之间以堆叠形式呈现，不会存在层叠。我们可以发现在Fig 2.1（c）中的Biscoe和Dream岛屿呈现的两个峰，来自于这两个岛屿中的两大企鹅种群——Gentoo，Chinstrap+Adelie（这两个种类的分布较为接近）分布导致。也就是说，鳍肢和企鹅种类的关联才是本质的因果关系。

1
2
ret = sns.displot(data, x="island", hue='species')
ret = sns.displot(data, x="island", hue='species', multiple="stack", discrete=False)

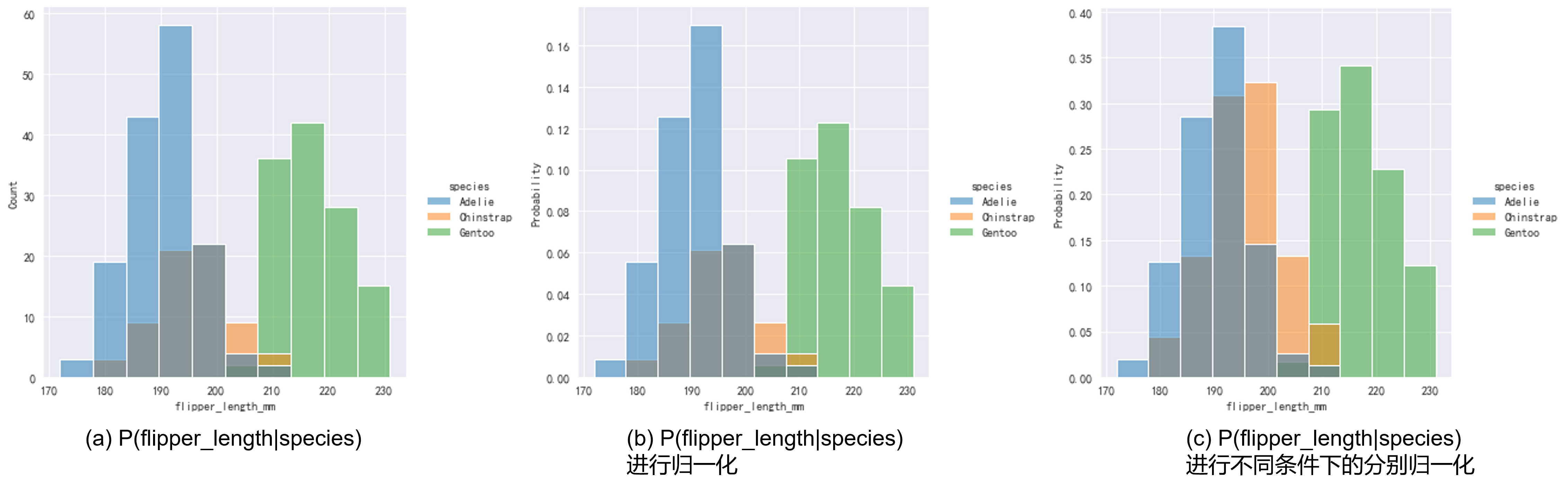
Fig 2.2 （a）一般形式的条件分布绘制，有时候由于柱形图的层叠，容易看不出清楚，此时可以采用stack模式，如（b）所示，此时不同柱形之间不会有层叠。

我们在Fig 1.2中说到过直方图的归一化，由于Fig 1.2中是单变量的分布归一化，因此体现到图中只是纵坐标的尺度变化，而整个图的形状是不会有变化的。在条件直方图中，我们可以将common_norm设置为False，此时进行归一化会将不同条件下的条件分布进行独立的归一化，如Fig 2.3所示，其中（a）和（b）只有纵坐标上的区别，而（c）是将不同条件下的条件分布进行各自的归一化。

1
2
3
ret = sns.displot(data, x="flipper_length_mm", hue='species')
ret = sns.displot(data, x="flipper_length_mm", hue='species', stat="probability")
ret = sns.displot(data, x="flipper_length_mm", hue='species', stat="probability", common_norm=False)

Fig 2.3 （a）条件分布原图；（b）对条件分布进行归一化，不考虑不同条件下的区别；（c）进行不同条件下的分别归一化。

核密度估计曲线

直方图对数据进行分箱后，统计每个箱子中的数据点频次，因此绘制出来的直方图是离散的柱形图，即便数据是连续型数据。有什么方法可以更好地体现数据的连续性质呢？核密度估计（Kernel Density Estimation，KDE）是一种可行的方法，我们假设每个数据点都是对数据分布的一次随机采样，采样自均值为观察值，方差为的核分布，如公式(3-1)所示，我们对所有数据点的核密度估计曲线进行叠加，得到整个数据分布的核密度估计曲线。我们的核分布通常可以采用高斯分布，如公式(3-2)所示。

如Fig 3.1所示，在给定了6个观察值，绘制出的直方图如Fig 3.1（a）所示，如Fig 3.1（b）所示，其中的红色曲线表示每个样本的高斯核密度估计，叠加起来得到蓝色曲线，为整个数据分布的核密度估计曲线。

样本123456
观察值-2.1-1.3-0.41.95.16.2

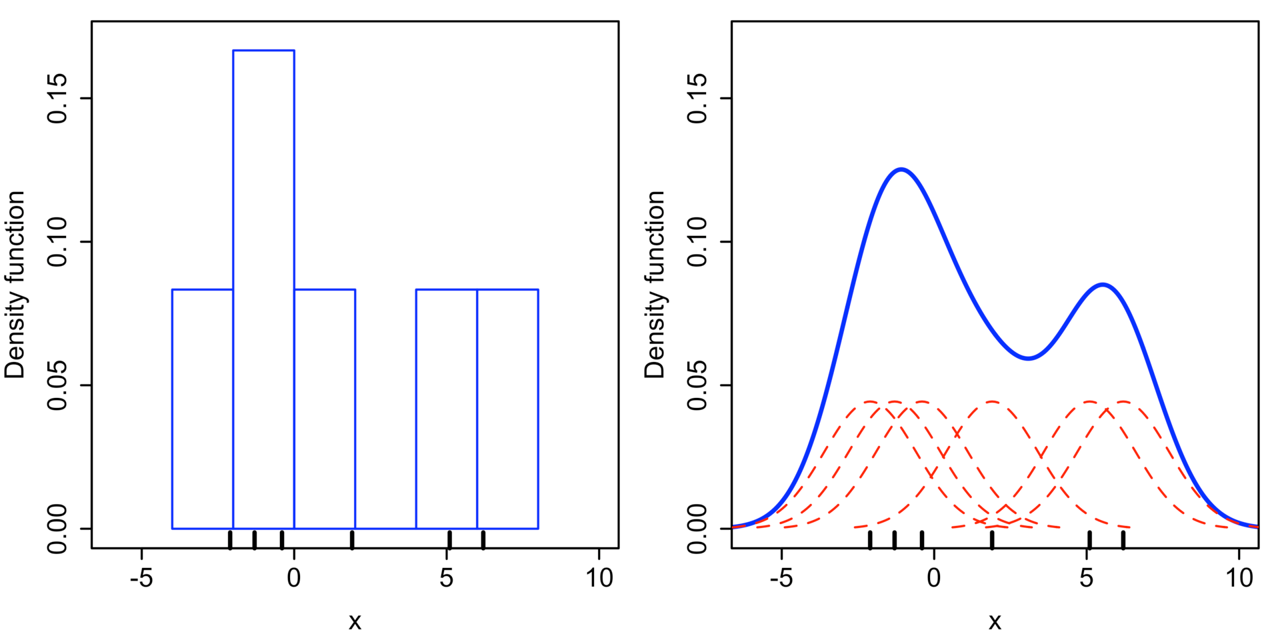
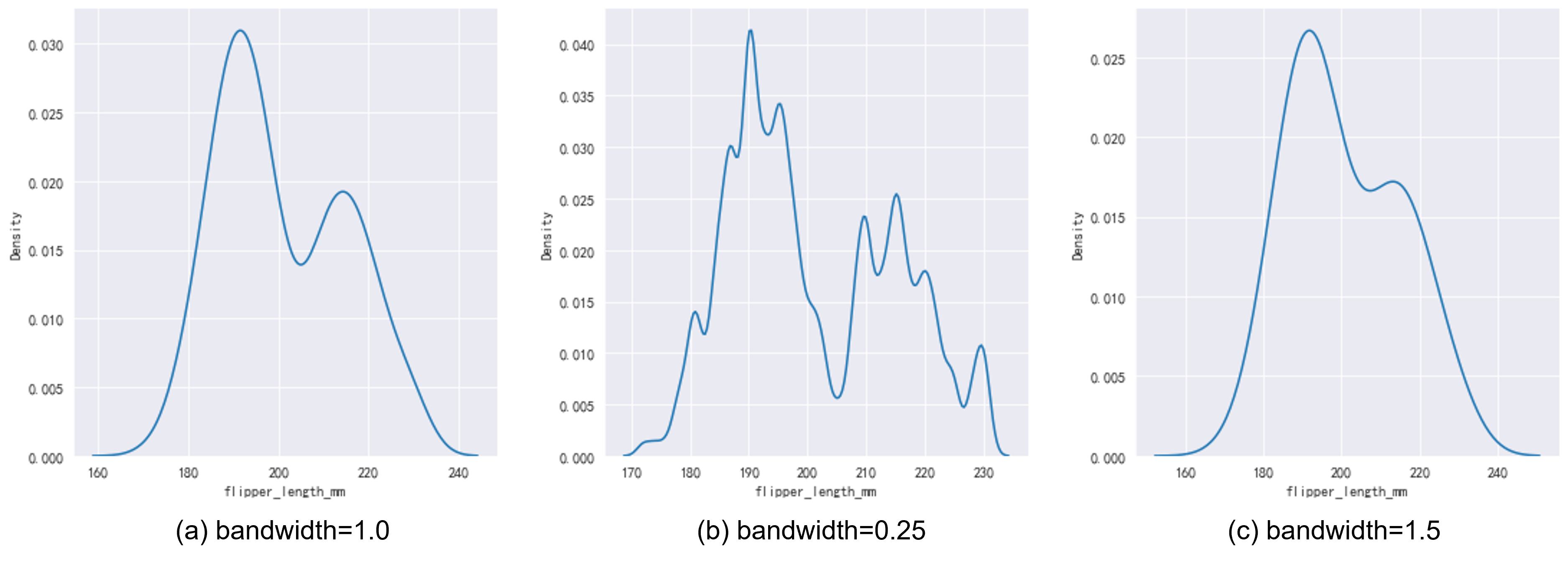
Fig 3.1 （a）直方图；（b）对每个样本进行核密度估计，然后叠加得到数据分布的拟合曲线。

回到我们的seaborn，我们通过设置参数kind="kde"进行设置，同时可以通过bw_adjust控制其方差，我们通常把此处的方差称之为带宽（bandwidth）。如Fig 3.2所示，我们发现不同的带宽下，核密度估计曲线的形状天差地别，Fig 3.2（b）中，过小的带宽可以看到分布的更多细节，但是也会收到更多数据噪声的影响，出现过多的毛刺。如Fig 3.2（c）所示，过大的带宽会使得曲线过于平滑，使得一些分布细节被掩饰了，比如其中的双峰分布就被平滑得看不出来了。

1
2
3
sns.displot(data, x="flipper_length_mm", kind="kde", bw_adjust=1)
sns.displot(data, x="flipper_length_mm", kind="kde", bw_adjust=0.25)
sns.displot(data, x="flipper_length_mm", kind="kde", bw_adjust=1.5)

Fig 3.2 不同的带宽参数对于核密度估计函数曲线的影响。

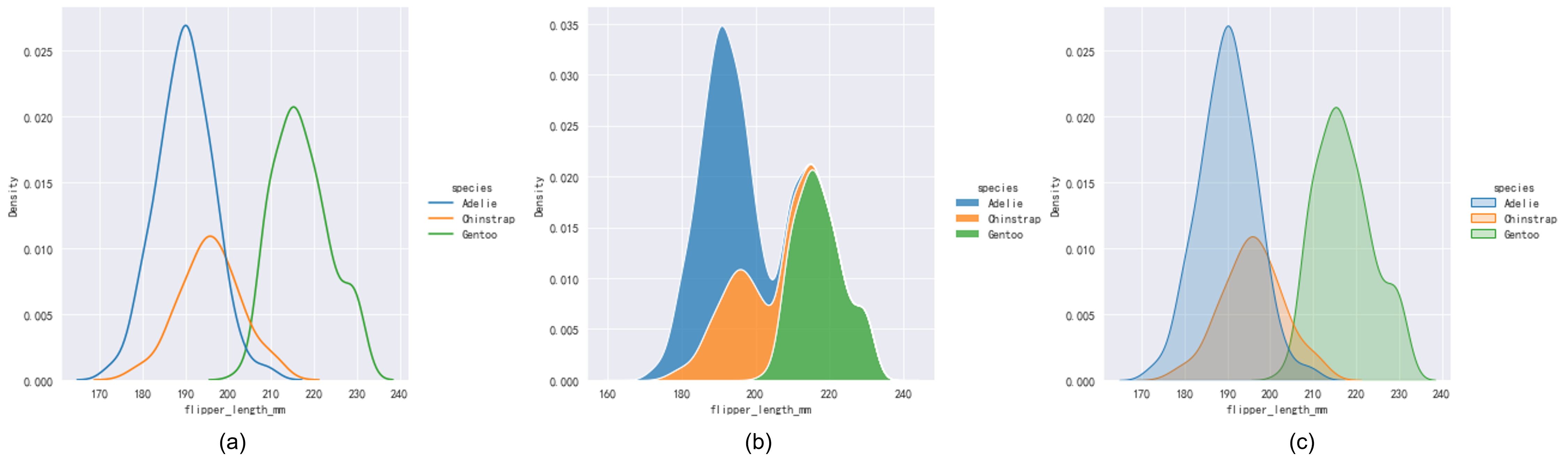
当然，核密度估计也可以在条件分布的情况下使用，如Fig 3.3所示，同样有几种不同的参数配置曲线的显式效果。

1
2
3
sns.displot(data, x="flipper_length_mm", hue="species", kind="kde")
sns.displot(data, x="flipper_length_mm", hue="species", kind="kde", multiple="stack")
sns.displot(data, x="flipper_length_mm", hue="species", kind="kde", fill=True)

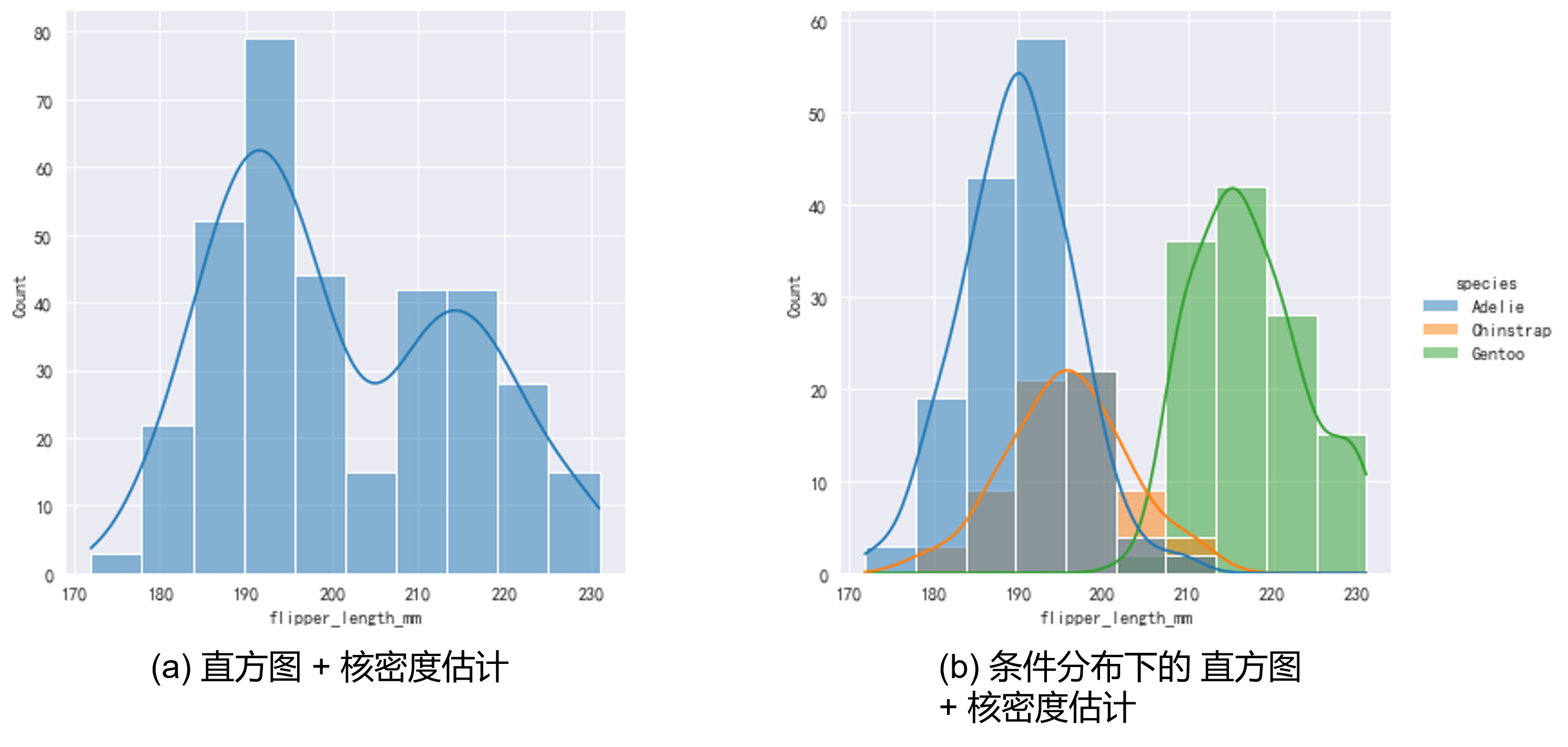
Fig 3.3 （a） 条件分布下的核密度估计曲线；（b）stack模式的条件分布核密度估计曲线；（c）填充曲线下面积的条件分布核密度估计曲线。

可以将直方图和核密度估计曲线绘制在同一张图中以便于分析，如Fig 3.4所示。

1
2
sns.displot(data, x="flipper_length_mm", kde=True)
sns.displot(data, x="flipper_length_mm", hue="species", kde=True)

Fig 3.4 将直方图和核密度估计曲线绘制在同一张图中。

箱型图

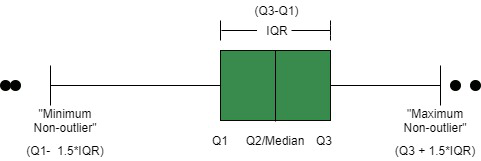
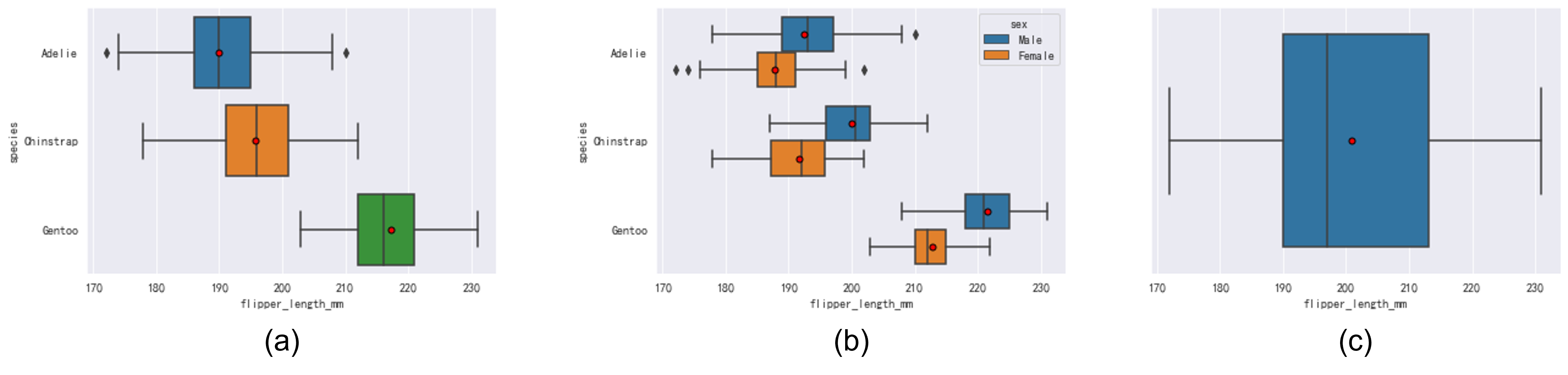
直方图和核密度估计都太“重”了，很多时候在刚接触某个数据集的时候，一些统计性指标就足够让我们对这份数据有足够的了解。常用的统计指标有：中位数（50分位线数），均值，方差，25分位线数，75分位线数等，而这些指标大多数情况可以从箱型图（Boxplot）中一目了然。如Fig 4.1所示，一个箱型图由五根线构成，Q1是25分位线，Q3是75分位线，指的是将数据从低到高排序（升序），前25%称之为25分位线，前75%称之为75分位线。Q3-Q1称之为四分位距（Inter Quartile Range，IQR），Q2表示50分位线，也即是中位线，小于Q1-1.5IQR 和 大于 Q3+1.5IQR的数据称之为离群点。

Fig 4.1 箱型图的几种基本分位线。

如Fig 4.2所示，我们可以用seaborn绘制箱型图，其中用红点表示均值，可以发现Fig 4.2（a）其实绘制了条件分布下的箱型图，当然也可以和Fig 4.2（c）一样绘制单变量的箱型图，这种也是我们最常见到的形式。如Fig 4.2（b）所示，我们还可以绘制2个条件下的箱型图，也即是。通过箱型图，我们可以非常直观地观察到不同数据分布之间的差别，是一种轻量化的数据分布分析方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
sns.boxplot(data=data, 
            x="flipper_length_mm", y='species', 
            showmeans=True,
            meanprops={"marker":"o",
                       "markerfacecolor":"red", 
                       "markeredgecolor":"black",
                      "markersize":"5"})
sns.boxplot(data=data, 
            x="flipper_length_mm", y='species', hue='sex',
            showmeans=True,
            meanprops={"marker":"o",
                       "markerfacecolor":"red", 
                       "markeredgecolor":"black",
                      "markersize":"5"})
sns.boxplot(data=data, 
            x="flipper_length_mm", 
            showmeans=True,
            meanprops={"marker":"o",
                       "markerfacecolor":"red", 
                       "markeredgecolor":"black",
                      "markersize":"5"})

Fig 4.2 （a）箱型图；（b）多个条件下的箱型图；（c）单变量箱型图。

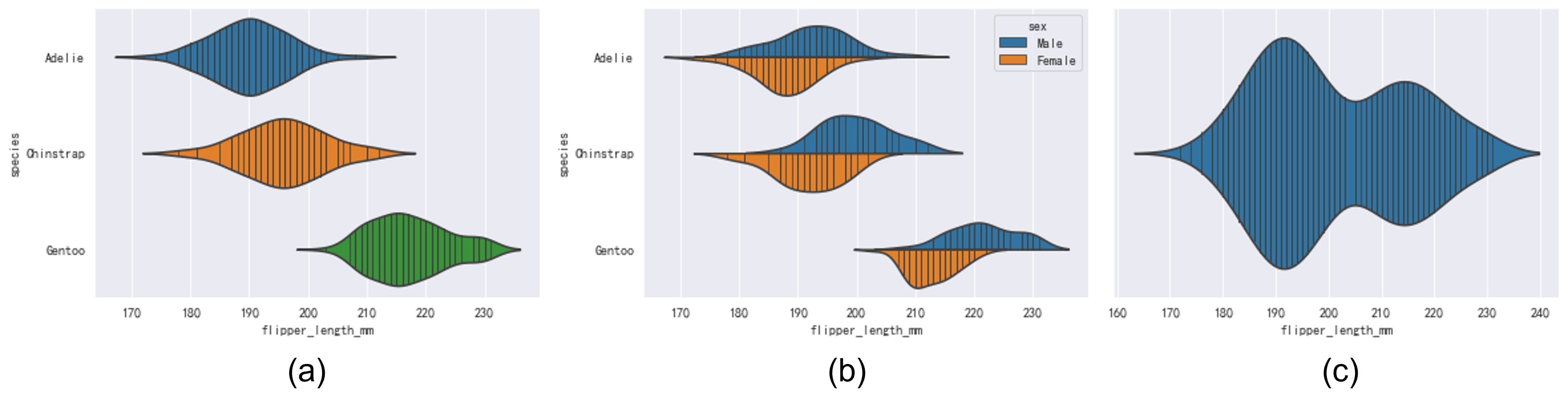
提琴图

箱型图可以提供数据的直观印象，为了进一步分析数据，我们还是需要引入分布曲线。我们希望可以以箱型图的形式，同时把数据分布也可视化出来，这样我们既可以复用箱型图得到的结论，而且可以进一步探索数据分布的细致区别。提琴图（Violin Plot）就是为此设计的，如Fig 5.1所示，其将数据的核密度估计曲线以类似于箱型图的排版进行展示，其中的每条黑色竖线是每个真实的样本点数据。注意到提琴图本质是核密度估计曲线，因此如果样本数据过少其曲线是不准确的，所以通常我们会把样本点也绘制出来（也即是黑色竖线），以判断数据数量是否会过于稀疏导致KDE不置信。

1
2
3
sns.violinplot(data=data, x="flipper_length_mm", y='species', inner="stick")
sns.violinplot(data=data, x="flipper_length_mm", y='species', hue='sex', split=True, inner="stick")
sns.violinplot(data=data, x="flipper_length_mm", inner="stick")

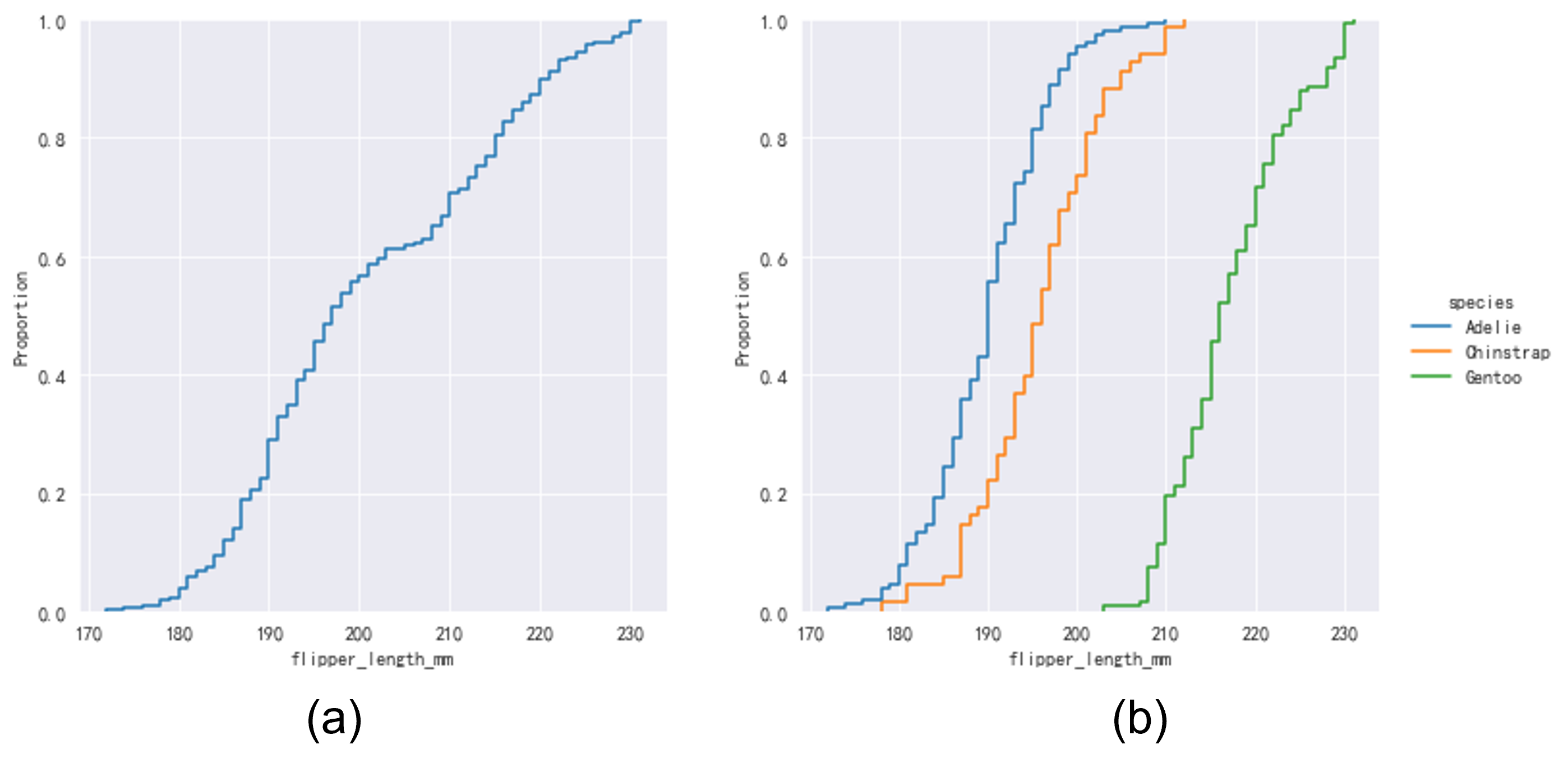
Fig 5.1 提琴图的不同形式，（a）提琴图；（b）两个条件下的提琴图；（c）单变量提琴图。

累积分布函数曲线

直方图需要选择合适的分箱数，而KDE需要选择合适的带宽，否则可能会影响数据分布的可视化效果进而影响分析。有没有一种方法可以不用选择任何参数就能表征数据的分布特性呢？经验累积分布函数（Empirical Cumulative Distribution Function，ECDF）也许是一种可行的选择。累积分布函数（Cumulative Distribution Function，CDF）对概率分布进行积分或者求和得到，如公式（6-1）所示。当对实际数据进行处理时候，由于我们的数据有限且来自于实际观察，因此我们通常称之为“经验”[2]，并且ecdf是采用求和，而不是积分。 如Fig 6.1所示，ecdf曲线是一个单调递增的曲线，其会考虑每一个观察到的数据点，不需要指定其他额外的参数，如Fig 6.1（b）所示，我们也可以绘制条件分布下的ecdf。ECDF的缺点在于不如直方图和核密度估计一样直观地表征了数据分布，但是理论上ECDF同样可以“坍缩”到概率分布，如公式(6-2)所示 

1
2
sns.displot(data, x="flipper_length_mm", kind="ecdf")
sns.displot(data, x="flipper_length_mm", hue="species", kind="ecdf")

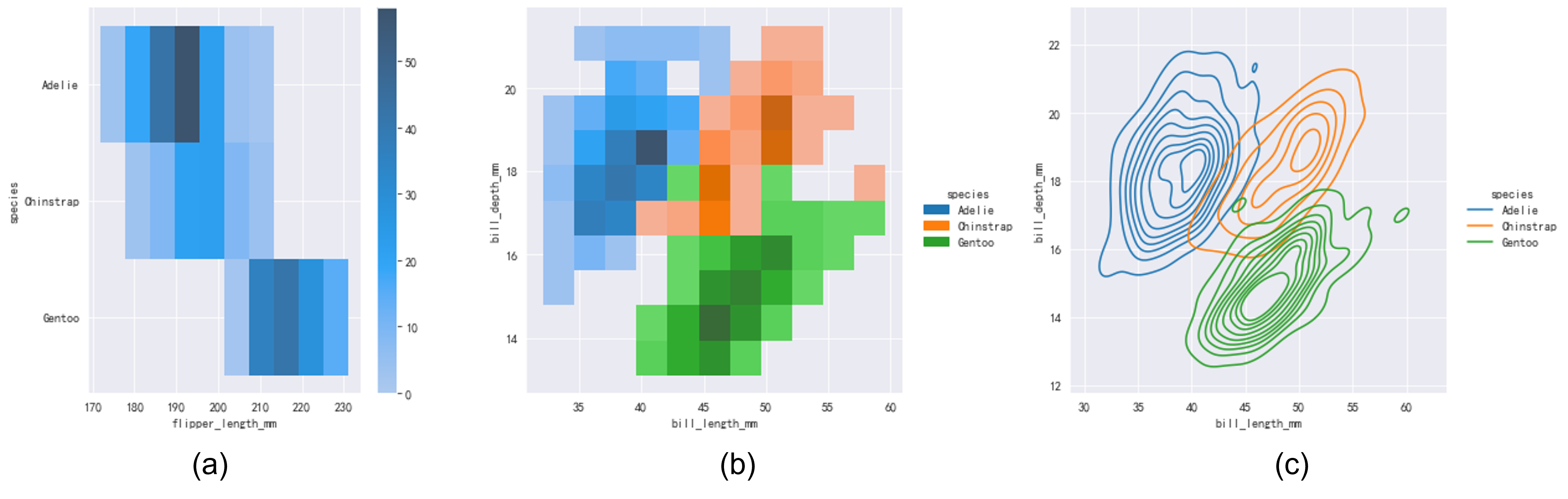
Fig 6.1 ECDF曲线，（a）单变量的ECDF曲线；（b）条件分布下的ECDF曲线。

二元直方图

有时候我们需要考察数据的联合概率分布，比如，此时可以绘制二元直方图。我们可以指定displot()的y参数，绘制两元变量的直方图。这种类型的直方图类似于热值图（heatmap），以颜色的深浅表示数值的大小。如Fig 7.1（c）所示，同样可以指定kind参数进而绘制二元核密度估计曲线。在指定了hue的情况下，同样可以实现条件分布的绘制。

1
2
3
sns.displot(data, x="flipper_length_mm", y="species",cbar=True)
sns.displot(data, x="bill_length_mm", y="bill_depth_mm", hue="species")
sns.displot(data, x="bill_length_mm", y="bill_depth_mm", hue="species", kind="kde")

Fig 7.1 二元直方图以及二元核密度估计曲线。

联合概率分布 和 边缘概率分布曲线

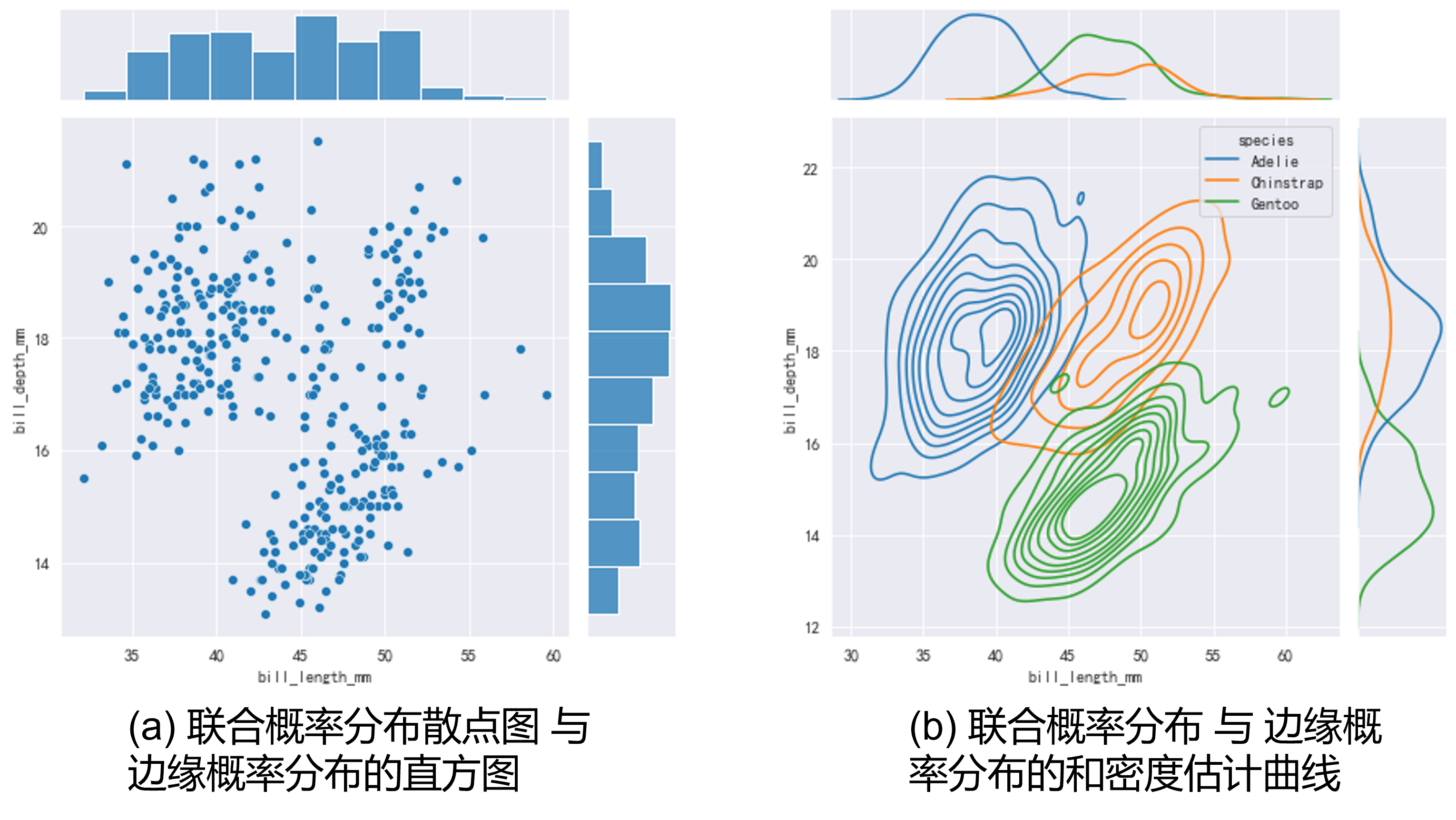
考察二元变量的联合概率分布，采用散点图（scatter plot）也是一种不错的选择，如Fig 8.1所示，可以将通过散点图的形式进行可视化，直观地考察两个变量之间的相关关系。散点图上面的直方图和右边的直方图分别是和分布的直方图，在这种情形下，我们称之为边缘概率分布曲线（Marginal Distribution），其计算公式见(8-1)。 我们也可以对联合概率分布的散点图和边缘概率分布的直方图进行核密度估计，如Fig 8.1（b）所示。

1
2
3
4
5
6
sns.jointplot(data=data, x="bill_length_mm", y="bill_depth_mm")
sns.jointplot(
    data=data,
    x="bill_length_mm", y="bill_depth_mm", hue="species",
    kind="kde"
)

Fig 8.1 联合概率分布与边缘概率分布的可视化。

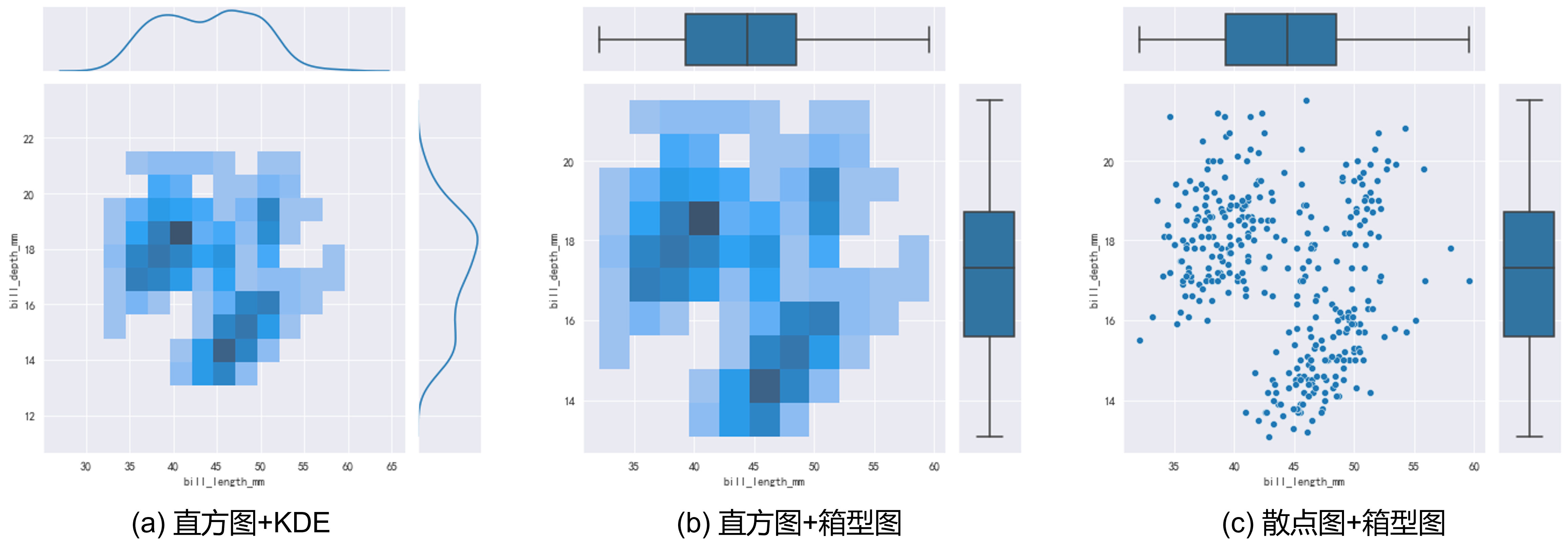
通过使用seaborn的JointGrid功能，可以对联合概率分布和边缘概率分布的表示形式进行自定义组合（散点图，KDE，箱型图等），如Fig 8.2所示。

1
2
3
4
5
6
7
8
9
10
11
g = sns.JointGrid(data=data, x="bill_length_mm", y="bill_depth_mm")
g.plot_joint(sns.histplot)
g.plot_marginals(sns.kdeplot)

g = sns.JointGrid(data=data, x="bill_length_mm", y="bill_depth_mm")
g.plot_joint(sns.histplot)
g.plot_marginals(sns.boxplot)

g = sns.JointGrid(data=data, x="bill_length_mm", y="bill_depth_mm")
g.plot_joint(sns.scatterplot)
g.plot_marginals(sns.boxplot)

Fig 8.2 通过JointGrid进行直方图，KDE，散点图，箱型图的组合。

Reference

[1]. https://seaborn.pydata.org/tutorial/distributions.html#plotting-univariate-histograms

[2]. https://blog.csdn.net/LoseInVain/article/details/78746520, 经验误差，泛化误差