笔者在[1,2]中已经对darknet如何进行配置解析进行了讲解，现在我们需要将解析出来的配置进行对应的网络层构建。

FesianXu 20201120 at UESTC

前言

笔者在[1,2]中已经对darknet如何进行配置解析进行了讲解，现在我们需要将解析出来的配置进行对应的网络层构建。如有谬误请联系指出，本文遵守CC 4.0 BY-SA版权协议，转载请联系作者并注明出处，谢谢。

联系方式：

e-mail: FesianXu@gmail.com

QQ: 973926198

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

微信公众号：

在阅读本文之前，请确保已经阅读过以下系列文章，否则可能会有前置知识点的缺失：

本文接着以上的文章，继续讨论如何根据解析出来的网络配置去构建网络结构network。为了讨论一致性，此处需要贴出[2]中的code 1.1，后续需要参考这段代码进行讨论。

network *parse_network_cfg(char *filename)
{
    list *sections = read_cfg(filename); // 解析cfg配置文件，返回配置链表，如Fig 1.1所示
    node *n = sections->front; // 获取sections的首节点，一般是[network]或者[net]类型的section
    if(!n) error("Config file has no sections"); // 判断是否存在section
    network *net = make_network(sections->size - 1); //构建network,其中的sections->size是包括了[net]之后的长度，因此要减去1，一共有sections->size-1层。
    net->gpu_index = gpu_index;
    size_params params; // 该数据结构承担了初始化网络结构，参数的重任，该结构体的定义如code 1.2所示。

    section *s = (section *)n->val;
    // 取得第一个section节点的指针，因为第一个section一般是一些全局的配置，具体见[1]。
    list *options = s->options; // 第一个section内容负载中的双向链表
    // 第一个section类型必须是[net]或者[network]
    if(!is_network(s)) error("First section must be [net] or [network]");
    // 如果没啥问题，就开始解析网络的全局配置，也即是[net]中的内容，将解析出的内容赋值到net数据结构中
    parse_net_options(options, net); 

    params.h = net->h;
    params.w = net->w;
    params.c = net->c;
    params.inputs = net->inputs;
    params.batch = net->batch;
    params.time_steps = net->time_steps;
    params.net = net;
    // 这一段都是在对对应的值进行赋值，没太多可说的

    size_t workspace_size = 0;
    // workspace_size 指明了所有层（layer）中最大的内存需求，从而提前开辟出整块内存以便后续计算，同一时间内，GPU或者CPU只有一个层在计算，因此只需要满足最大内存需求即可。
    n = n->next; // 我们已经把[net]结构体解析完啦，现在我们考虑之后的层，一般就是实际的神经网络层了。
    int count = 0;
    free_section(s); 
    fprintf(stderr, "layer     filters    size              input                output\n");
    while(n){  // 当 NULL == n 的时候退出解析
        params.index = count; // 每一层的计数器，从0开始
        fprintf(stderr, "%5d ", count);
        s = (section *)n->val; // 每一层的实际负载，也即是section本体
        options = s->options; // 实际section的双向链表，其中的元素
        layer l = {0}; // 解析出的section将初始化到layer中，此处先定义layer。
        LAYER_TYPE lt = string_to_layer_type(s->type); // 将字符串格式的层名，比如[convolutional]等解析为枚举类型的数据
        
        // 针对不同类型的层lt，有着不同的解析函数，格式为 parse_xxxx(options, params)，我们后续以卷积层为例子，其他层也是类似的。
        if(lt == CONVOLUTIONAL){
            l = parse_convolutional(options, params);
        }else if(lt == DECONVOLUTIONAL){
            l = parse_deconvolutional(options, params);
        }
        .... 
        // 为了简便，这里省略了很多相似的parse解析函数，分别解析不同的层
        else if(lt == DROPOUT){
            l = parse_dropout(options, params);
            l.output = net->layers[count-1].output;
            l.delta = net->layers[count-1].delta;
        }else{
            fprintf(stderr, "Type not recognized: %s\n", s->type);
        }
        
        l.clip = net->clip;
        l.truth = option_find_int_quiet(options, "truth", 0);
        ....
        // 这里省略了类似的参数解析过程
        l.learning_rate_scale = option_find_float_quiet(options, "learning_rate", 1);
        l.smooth = option_find_float_quiet(options, "smooth", 0);
        // 针对每个特定层，还可以指定其特定的学习率learning_rate，是否停止梯度stopbackward,平滑smooth,保存参数与否dontsave，加载参数与否dontload,等细节参数，这些参数将会在该层覆盖全局[net]的设置。这里的代码在解析这些参数。
        
        option_unused(options); // 将没有使用到的参数打印（因为有可能cfg文件写错了，某些层不需要某些参数，但是又多写了，这里需要提示出来）
        net->layers[count] = l; // 将解析得到的layer赋值到network中。
        if (l.workspace_size > workspace_size) workspace_size = l.workspace_size;
        // 每个特定层，需要的内存空间是不一样的，这个在定义某个层的时候是需要预先定义（计算）出来的，通过这个代码纪录整个网络需要的最大内存空间。
        free_section(s); // 释放解析临时内存
        n = n->next; // 走，哥们我们去下一个section
        ++count;
        if(n){
            params.h = l.out_h;
            params.w = l.out_w;
            params.c = l.out_c;
            params.inputs = l.outputs;
        }
    }
    
    free_list(sections);
    layer out = get_network_output_layer(net); // 取得输出层的句柄
    net->outputs = out.outputs;
    net->truths = out.outputs;
    if(net->layers[net->n-1].truths) net->truths = net->layers[net->n-1].truths;
    net->output = out.output;
    // 网络的输出就是输出层的最终输出
    net->input = calloc(net->inputs*net->batch, sizeof(float));
    // 给网络输入分配空间,大小取决于每个样本的维度net->inputs和批次大小net->batch
    net->truth = calloc(net->truths*net->batch, sizeof(float));
    // ground truths 的内存分配
    if(workspace_size){
        //printf("%ld\n", workspace_size);
    	net->workspace = calloc(1, workspace_size);
    }
    // 正如之前说的，在任意时刻 GPU或者CPU中只有一个层在运行，因此只需要预先分配所有层的最大内存需求即可了。
    return net;
}

code a1. parse_network_cfg的函数定义，注意到为了显示简便，省略了许多重复类似的语句，读者可以查阅源代码或者根据上下文得知含义。

make_network

make_network处在code a1中#6行[3]，是用来初始化一个network结构体的。代码很简单，如code 1.1所示

network *make_network(int n)
{
    network *net = calloc(1, sizeof(network));
    net->n = n; // 一共有多少网络层，不包括[net]或者[network]字段的section
    net->layers = calloc(net->n, sizeof(layer)); // 对所有层进行内存分配
    net->seen = calloc(1, sizeof(size_t));  
    net->t    = calloc(1, sizeof(int)); 
    net->cost = calloc(1, sizeof(float)); 
    return net;
}

code 1.1 make_network的定义，其中主要是对若干元素进行内存分配，注意到net->n是不包括[net]或者[network]字段的。

正如在[1]中谈到的，layer结构体内包含了所有神经网络层（卷积层，转置卷积层，激活层等等）的所有相关参数，因此可以看成是一个超大的数据结构，因此只需要初始化该数据就足够了。当然，这样设计出来的数据结构过于冗余，这又是后话了。

make_convolutional_layer

make_convolutional_layer在parse_convolutional中作为函数被调用，该函数用于构建卷积层，代码如code 2.1，同样为了简便起见，去掉了所有和CUDA和CUDNN相关的代码段，假设代码只运行在CPU上。

convolutional_layer make_convolutional_layer(int batch, int h, int w, int c, int n, int groups, int size, int stride, int padding, ACTIVATION activation, int batch_normalize, int binary, int xnor, int adam)
{
    int i;
    convolutional_layer l = {0};
    l.type = CONVOLUTIONAL;

    l.groups = groups;
    l.h = h;
    l.w = w;
    l.c = c;
    l.n = n; // 滤波器的数量
    l.binary = binary;
    l.xnor = xnor;
    l.batch = batch;
    l.stride = stride;
    l.size = size;
    l.pad = padding;
    l.batch_normalize = batch_normalize;
    // 卷积层的一系列超参数赋值

    l.weights = calloc(c/groups*n*size*size, sizeof(float));
    l.weight_updates = calloc(c/groups*n*size*size, sizeof(float));
    // 对权值参数进行内存空间分配

    l.biases = calloc(n, sizeof(float));
    l.bias_updates = calloc(n, sizeof(float));
    // 对偏置参数进行内存空间分配

    l.nweights = c/groups*n*size*size;
    l.nbiases = n;
    // 权值参数和偏置参数的参数量大小

    float scale = sqrt(2./(size*size*c/l.groups));    
    for(i = 0; i < l.nweights; ++i) l.weights[i] = scale*rand_normal();
    // 权值参数随机初始化
    int out_w = convolutional_out_width(l);
    int out_h = convolutional_out_height(l);
    // 确定卷积输出尺寸大小，具体见公式见(2.1)和code 2.2
    l.out_h = out_h;
    l.out_w = out_w;
    l.out_c = n;  // 滤波器的数量，相当于输出通道数`channel_out`
    l.outputs = l.out_h * l.out_w * l.out_c; // 输出特征图的总维度
    l.inputs = l.w * l.h * l.c; // 输入特征图的总维度

    l.output = calloc(l.batch*l.outputs, sizeof(float)); // 对一个批次的输出特征图进行内存分配
    l.delta  = calloc(l.batch*l.outputs, sizeof(float)); // 对一个批次的更新中间量（见[1]）进行内存分配，每个特征输出都对应一个，因此和l.outputs的维度一致。

    l.forward = forward_convolutional_layer;
    l.backward = backward_convolutional_layer;
    l.update = update_convolutional_layer;
    // 注册前向，反向和更新回调函数。
	
    if(batch_normalize){
        l.scales = calloc(n, sizeof(float));
        l.scale_updates = calloc(n, sizeof(float));
        for(i = 0; i < n; ++i){
            l.scales[i] = 1;
        }

        l.mean = calloc(n, sizeof(float));
        l.variance = calloc(n, sizeof(float));

        l.mean_delta = calloc(n, sizeof(float));
        l.variance_delta = calloc(n, sizeof(float));

        l.rolling_mean = calloc(n, sizeof(float));
        l.rolling_variance = calloc(n, sizeof(float));
        l.x = calloc(l.batch*l.outputs, sizeof(float));
        l.x_norm = calloc(l.batch*l.outputs, sizeof(float));
    } // batch_norm 相关定义
    if(adam){
        l.m = calloc(l.nweights, sizeof(float));
        l.v = calloc(l.nweights, sizeof(float));
        l.bias_m = calloc(n, sizeof(float));
        l.scale_m = calloc(n, sizeof(float));
        l.bias_v = calloc(n, sizeof(float));
        l.scale_v = calloc(n, sizeof(float));
    } // adam相关定义
    l.workspace_size = get_workspace_size(l); // 获取该层的workspace大小，见code 2.3
    l.activation = activation;

    fprintf(stderr, "conv  %5d %2d x%2d /%2d  %4d x%4d x%4d   ->  %4d x%4d x%4d  %5.3f BFLOPs\n", n, size, size, stride, w, h, c, l.out_w, l.out_h, l.out_c, (2.0 * l.n * l.size*l.size*l.c/l.groups * l.out_h*l.out_w)/1000000000.); // 自说明输出
    return l;
}

code 2.1 make_convolutional_layer的定义，其他类似层的定义也是相似的，函数名都为`make_xxx_layer`。

其中的convolutional_layer其实和layer是一致的，原因之前说过了，layer是一个冗余的超类。

1	typedef layer convolutional_layer;

代码中需要根据pad和width/height，kernel_size，stride去确定卷积输出的尺寸大小，计算方式见公式(2.1)和code 2.2。

int convolutional_out_height(convolutional_layer l)
{
    return (l.h + 2*l.pad - l.size) / l.stride + 1;
}

int convolutional_out_width(convolutional_layer l)
{
    return (l.w + 2*l.pad - l.size) / l.stride + 1;
}

code 2.2 计算卷积的输出尺寸大小。

1
2
3

static size_t get_workspace_size(layer l){
    return (size_t)l.out_h*l.out_w*l.size*l.size*l.c/l.groups*sizeof(float);
}

code 2.3 get_workspace_size 该函数计算给定的layer的内存需求，省略了关于CUDNN部分的代码。

代码中有三行很重要，是和后续的前向，反向计算，参数更新有关的：

l.forward = forward_convolutional_layer;
l.backward = backward_convolutional_layer;
l.update = update_convolutional_layer;
// 注册前向，反向和更新回调函数。

容易知道，每个不同的层，需要注册不同的这三类函数：

1
2
3

forward_xxx_layer(); // 用以定义该层的前向计算策略
backward_xxx_layer(); // 用以定义该层的反向计算策略
update_xxx_layer(); // 用以定义该层的参数更新策略

我们具体挑出来看看细节。

forward_xxx_layer

同样，我们以forward_convolutional_layer作为代表进行剖析，整个流程图如Fig 2.1所示，其中的im2col_cpu和gemm是作为卷积加速的一种常用方式，具体见[4]，以下为了讨论简便，假设l.groups = 1。

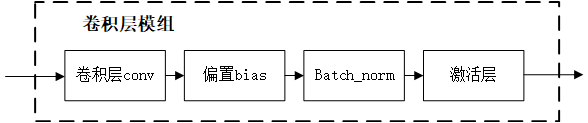
conv_forward

Fig 2.1 卷积层模组需要经过的若干个模块，包括卷积，偏置，BN和激活层等。

void forward_convolutional_layer(convolutional_layer l, network net)
{
    int i, j;
    fill_cpu(l.outputs*l.batch, 0, l.output, 1); // 初始化输出变量空间的值，将其全部初始化为0
    int m = l.n/l.groups;
    int k = l.size*l.size*l.c/l.groups;
    int n = l.out_w*l.out_h;
    // 这里group是深度可分离卷积(depthwise convolution)里面的内容
    for(i = 0; i < l.batch; ++i){
        for(j = 0; j < l.groups; ++j){
            float *a = l.weights + j*l.nweights/l.groups;
            // 计算权值的起始指针，按照不同的group区分
            float *b = net.workspace;
            float *c = l.output + (i*l.groups + j)*n*m;
            // 输出的对应指针偏移计算
            float *im =  net.input + (i*l.groups + j)*l.c/l.groups*l.h*l.w;
            // 输入对应指针偏移计算

            if (l.size == 1) {
                b = im; // 如果是1x1卷积，就不需要im2col
            } else {
                im2col_cpu(im, l.c/l.groups, l.h, l.w, l.size, l.stride, l.pad, b);
            }
            // 通过im2col将卷积转换成矩阵乘法运算
            gemm(0,0,m,n,k,1,a,k,b,n,1,c,n); // 通过GEMM计算矩阵乘法
        }
    }

    if(l.batch_normalize){
        forward_batchnorm_layer(l, net);
    } else {
        add_bias(l.output, l.biases, l.batch, l.n, l.out_h*l.out_w);
    }
    // 进行batch_norm 和 添加偏置计算
    activate_array(l.output, l.outputs*l.batch, l.activation); // 添加激活层
    if(l.binary || l.xnor) swap_binary(&l); // 二值化的权值，本文不考虑这个。
}

code 2.4 forward_convolutional_layer 的定义。

code 2.4中代码需要计算很多关于内存指针的偏移（因为物理内存上这些高阶张量都是线性排列的，具体高阶索引体现在特定的指针偏移上），比如#14和#16行都有(i*l.groups + j)这个偏移项，其实就是在考虑组别groups和不同批次batch对内存索引的影响，因为输入输出的特征图大小不同，因此后面接的系数当然也不同，分别是*n*m和*l.c/l.groups*l.h*l.w。

既然是卷积层的前向计算，其中最为关键的莫过于是如何进行卷积计算，我们首先关注im2col_cpu这个函数：

void im2col_cpu(float* data_im,
     int channels,  int height,  int width,
     int ksize,  int stride, int pad, float* data_col) 
{
    /*
    float* data_im: 输入的特征图指针，呈现线性排列，是拉直后的结果（物理内存就是线性的）
    int channels: 输入通道数
    int height, int width: 输入特征图的高度和宽度
    int ksize: 卷积核大小
    int stride: 步进
    int pad: 填充
    float* data_col: 经过im2col后的结果，将其保存在workspace中，因为能确保workspace的内存预分配大小符合最大内存需求，因此不担心其溢出。
    */
    int c,h,w;
    int height_col = (height + 2*pad - ksize) / stride + 1;
    int width_col = (width + 2*pad - ksize) / stride + 1;
    // 计算卷积核的尺寸参数
    int channels_col = channels * ksize * ksize; // 将通道拉直后的向量维度，见[4]中的讨论
    for (c = 0; c < channels_col; ++c) {
        int w_offset = c % ksize;
        int h_offset = (c / ksize) % ksize;
        int c_im = c / ksize / ksize;
        for (h = 0; h < height_col; ++h) {
            for (w = 0; w < width_col; ++w) {
                int im_row = h_offset + h * stride;
                int im_col = w_offset + w * stride;
                int col_index = (c * height_col + h) * width_col + w;
                data_col[col_index] = im2col_get_pixel(data_im, height, width, channels,
                        im_row, im_col, c_im, pad);
            }
        }
    }
    // 计算K^2C的内循环，给data_col赋值
}

code 2.5 im2col_cpu的定义。

函数的细节太多了，我们后续博文再更新讨论细节，就宏观来看，该函数将三阶张量展开成了矩阵data_col。然后通过通用矩阵乘法gemm进行卷积核的相乘，就得到了最终的卷积特征输出。gemm代码如code 2.6所示，其中细节比较多，我们暂且不讨论，从darknet的源码来看，作者似乎并没有进行太多的矩阵乘法优化（有待后续继续验证），只是进行了openMP的多线程优化。gemm的传入参数比较多，因为通用矩阵乘法是在对式子(2.2)进行计算的

void gemm(int TA, int TB, int M, int N, int K, float ALPHA, 
        float *A, int lda, 
        float *B, int ldb,
        float BETA,
        float *C, int ldc)
{
    /*
    参考式子(2.2)这里解释下参数
    int TA, int TB： 是否需要使用转置的传入矩阵。
    int M, int N, int K: 传入矩阵的尺寸
    float ALPHA: 式子(2.2)中的\alpha
    float BETA: 式子(2.2)中的\beta
    float *A: 传入矩阵A
    float *B: 传入矩阵B
    float *C: 传入矩阵C
    int lda, int ldb, int ldc: 表示的是leading dimension，也就是第一个维度的大小，可以看成是步进大小，用于做索引的时候确定元素的位置，比如add(A[i, j])=A+i*lda+j。这个细节我们可以暂时忽略。
    */
    gemm_cpu( TA,  TB,  M, N, K, ALPHA,A,lda, B, ldb,BETA,C,ldc);
}

code 2.6 gemm的参数表解释。

结合im2col和gemm，我们完成了卷积的前向计算。

backward_xxx_layer

梯度的反向传播计算的方向和前向计算相反，如Fig 2.1所示，将其反过来看得话，需要先求得激活层的梯度gradient_array()。笔者在之前的文章[5]中曾经简要介绍过卷积层的反向梯度传播，对于某个第输入通道，第输出通道，位置为的权值参数，我们有其导数为：总的来说，要考虑激活层的梯度，和卷积本身的梯度，然后将其相乘。具体代码解释见code 2.7的注释所示。

void backward_convolutional_layer(convolutional_layer l, network net)
{
    int i, j;
    int m = l.n/l.groups;
    int n = l.size*l.size*l.c/l.groups;
    int k = l.out_w*l.out_h;

    gradient_array(l.output, l.outputs*l.batch, l.activation, l.delta);
    // 实现逐个参数的【激活层】的梯度计算以及累加，其中的l.delta可以实现训练过程中的梯度累加，也即是所谓的敏感度图sensitive map，见code 2.8，因为是反向传播因此由最底层的激活层开始计算
    // 梯度累积通过l.delta进行传递

    if(l.batch_normalize){
        backward_batchnorm_layer(l, net);
    } else {
        backward_bias(l.bias_updates, l.delta, l.batch, l.n, k);
    }
    // 判断是否有bn层，进一步计算batch_norm的梯度或者bias的梯度，backward_batchnorm_layer内部包含了bias梯度反传

    for(i = 0; i < l.batch; ++i){
        for(j = 0; j < l.groups; ++j){
            float *a = l.delta + (i*l.groups + j)*m*k;
            float *b = net.workspace;
            float *c = l.weight_updates + j*l.nweights/l.groups;
			
            float *im  = net.input + (i*l.groups + j)*l.c/l.groups*l.h*l.w;
            float *imd = net.delta + (i*l.groups + j)*l.c/l.groups*l.h*l.w;
            // 类似于前向传播，但是此时要考虑敏感性图(l.delta)变量了，因为需要累积梯度

            if(l.size == 1){
                b = im;
            } else {
                im2col_cpu(im, l.c/l.groups, l.h, l.w, 
                        l.size, l.stride, l.pad, b);
            } // 如果是1x1卷积，则不需要im2col，如果不是，通过im2col将im转换为col形式的矩阵b。b此时是workspace。im是上一层的输出，即是本层的输入。

            gemm(0,1,m,n,k,1,a,k,b,k,1,c,n);
            // 见公式(2.4)，此处进行权值更新，激活层梯度是a，基础量是c，b是梯度
			
            // 此处进行workspace的更新，保存当前梯度累积结果，以便于后续网络的训练。
            if (net.delta) {
                a = l.weights + j*l.nweights/l.groups;
                b = l.delta + (i*l.groups + j)*m*k;
                c = net.workspace;
                if (l.size == 1) {
                    c = imd;
                }

                gemm(1,0,n,k,m,1,a,n,b,k,0,c,k);

                if (l.size != 1) {
                    col2im_cpu(net.workspace, l.c/l.groups, l.h, l.w, l.size, l.stride, l.pad, imd);
                } // 如果不是1x1卷积，那么通过col2im将其转换为张量结构。
            }
        }
    }
}

code 2.7 backward_convolutional_layer 卷积层的反向梯度传播计算。

更新参数的增量的公式如(2.4)所示，注意到此时还没有进行参数更新，只是进行参数更新量的计算而已，后续还需要考虑学习率进行衰减。其中的是激活层梯度，是卷积层梯度，是积累到当前层的参数更新量。

code 2.8是计算激活层梯度的过程。

void gradient_array(const float *x, const int n, const ACTIVATION a, float *delta)
{
    int i;
    for(i = 0; i < n; ++i){
        delta[i] *= gradient(x[i], a); // 计算激活层的梯度，并进行累积
    }
} 

float gradient(float x, ACTIVATION a)
{
    switch(a){
        case LINEAR:
            return linear_gradient(x);
        case LOGISTIC:
            return logistic_gradient(x);
		... // 省略了其他类似激活层的梯度
        case LHTAN:
            return lhtan_gradient(x);
    }
    return 0;
}

code 2.8 gradient_array 的定义，其中查阅gradient可以得到某个特定激活层的梯度（比如relu,linear,sigmoid等）。

update_xxx_layer

在backward_xxx_layer层只计算了反向传播过程中的基于梯度考虑的参数更新量，后续在真正的参数更新过程中，还需要结合优化器的学习策略进行参数更新量的调整，这些都定义在了update_xxx_layer函数中，如code 2.9所示。

void update_convolutional_layer(convolutional_layer l, update_args a)
{
    float learning_rate = a.learning_rate*l.learning_rate_scale; // 真实的学习率需要考虑衰减
    float momentum = a.momentum; // SGD的动量
    float decay = a.decay; 
    int batch = a.batch;

    axpy_cpu(l.n, learning_rate/batch, l.bias_updates, 1, l.biases, 1);
    scal_cpu(l.n, momentum, l.bias_updates, 1);
    // 考虑bias的更新

    if(l.scales){
        axpy_cpu(l.n, learning_rate/batch, l.scale_updates, 1, l.scales, 1);
        scal_cpu(l.n, momentum, l.scale_updates, 1);
    }
    // 考虑scale的更新以及动量的更新

    axpy_cpu(l.nweights, -decay*batch, l.weights, 1, l.weight_updates, 1);
    axpy_cpu(l.nweights, learning_rate/batch, l.weight_updates, 1, l.weights, 1);
    scal_cpu(l.nweights, momentum, l.weight_updates, 1);
    // 考虑weights的更新
}
void axpy_cpu(int N, float ALPHA, float *X, int INCX, float *Y, int INCY)
{
    int i;
    for(i = 0; i < N; ++i) Y[i*INCY] += ALPHA*X[i*INCX];
}

void scal_cpu(int N, float ALPHA, float *X, int INCX)
{
    int i;
    for(i = 0; i < N; ++i) X[i*INCX] *= ALPHA;
}

code 2.9 更新参数值的过程，需要结合具体的优化器更新策略。

注意：其中axpy_cpu和scal_cpu都是BLAS中的命名方式，表示向量化数值运算，其中axpy_cpu表示a x plus y，也就是，而scal_cpu则是scale，即是。

从中可发现，对于biases的更新策略是：

其中的是真实学习率learning_rate，是批次大小batch size，是bias_updates量，是动量momentum。

对于weights的更新策略是：符号表示的含义也是类似的，其中是衰减量decay。

Reference

[1]. [darknet源码系列-1] darknet源码中的常见数据结构 : https://fesian.blog.csdn.net/article/details/109779812

[2]. [darknet源码系列-2] darknet源码中的cfg解析 : https://fesian.blog.csdn.net/article/details/109863764

[3]. https://github.com/pjreddie/darknet/blob/4a03d405982aa1e1e911eac42b0ffce29cc8c8ef/src/parser.c#L747

[4]. [卷积算子加速] im2col优化: https://fesian.blog.csdn.net/article/details/109906065

[5]. https://zhuanlan.zhihu.com/p/158736917