最近笔者工作中用到了GBRank模型,其中用到了GBDT梯度提升决策树,原论文的原文并不是很容易看懂,在本文纪录下GBDT的一些原理和个人理解,作为笔记。
前言
最近笔者工作中用到了GBRank模型[1],其中用到了GBDT梯度提升决策树,原论文的原文并不是很容易看懂,在本文纪录下GBDT的一些原理和个人理解,作为笔记。如有谬误请联系指出,本文遵守CC 4.0 BY-SA版权协议,转载请联系作者并注明出处,谢谢。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号:

梯度提升决策树(Gradient Boost Decision Tree,GBDT)是一种通过梯度提升策略去提高决策树性能表现的一种树模型设计思想,本文集中讨论的是GBDT在回归中的应用。对于一个数据集
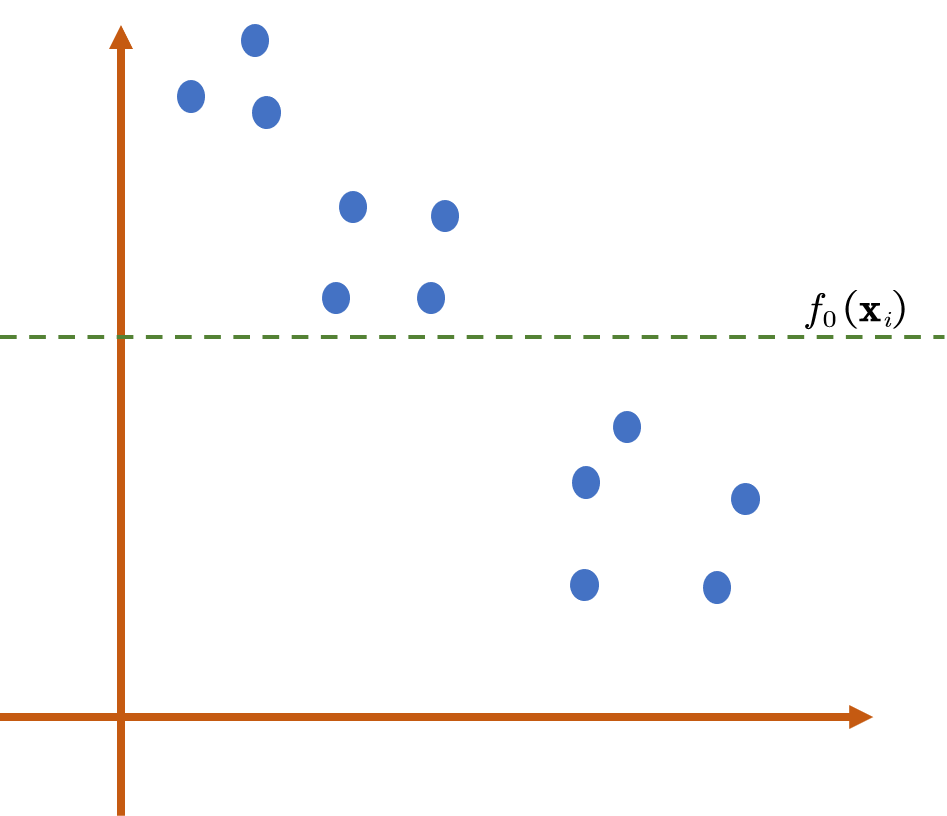
接下来我们得考虑如何去更新模型,在得到了
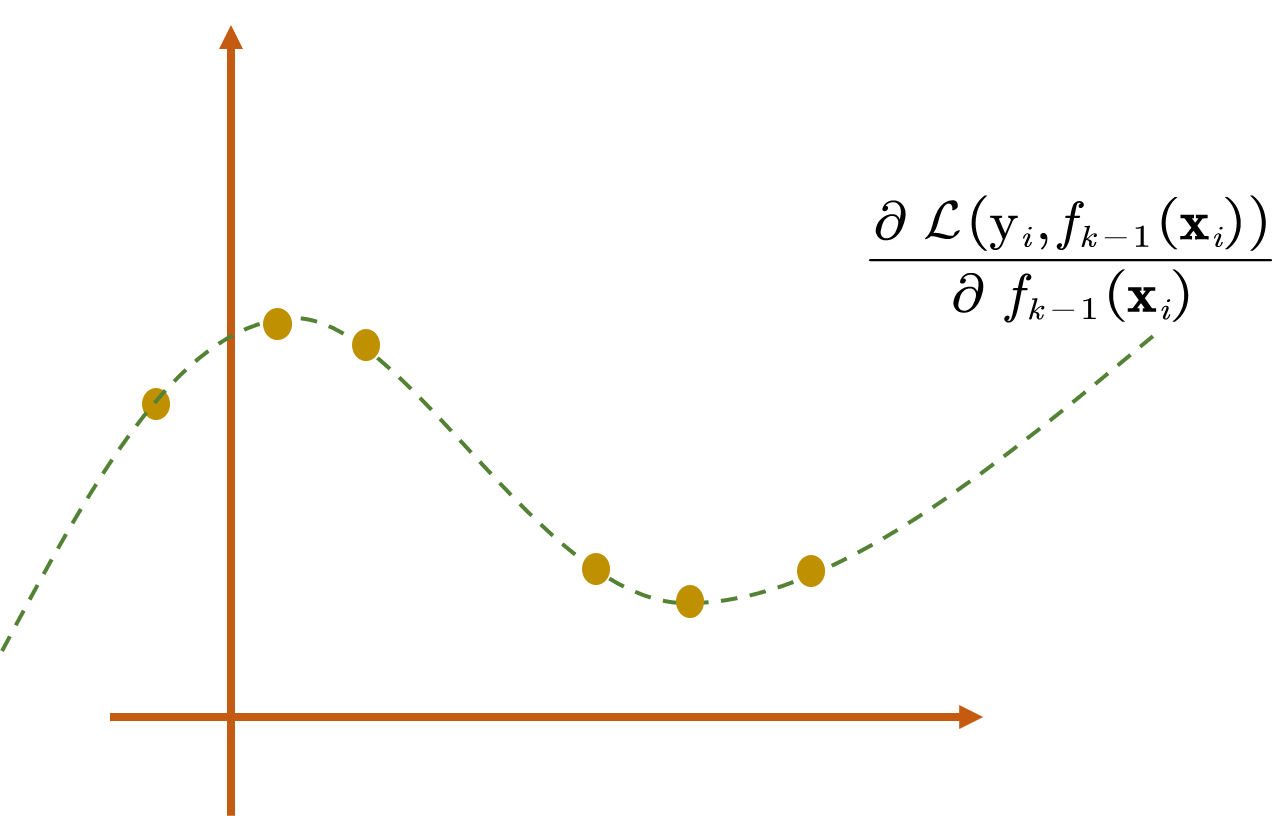
注意到得到的CART树模型
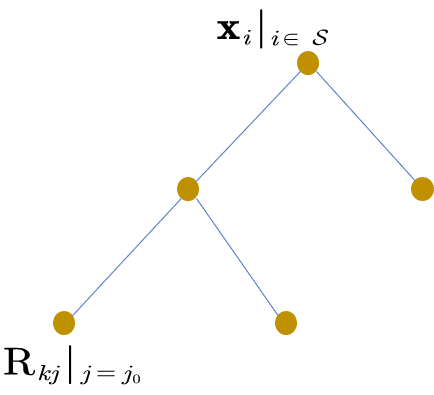
此时我们便有:
因此,如果当损失函数为MSE函数时,可以表现为是用多棵CART树模型对残差的不断拟合,但是如果当损失函数不是MSE时,则不能这样解释。
Reference
[1]. Zheng, Z., Chen, K., Sun, G., & Zha, H. (2007, July). A regression framework for learning ranking functions using relative relevance judgments. In Proceedings of the 30th annual international ACM SIGIR conference on Research and development in information retrieval (pp. 287-294).