本文作为笔者在学习搜索系统中时候遇到的一些指标以及其含义，计算方式的笔记。

FesianXu 20210131 at Baidu intern

前言

本文作为笔者在学习搜索系统中时候遇到的一些指标以及其含义，计算方式的笔记。如有谬误请联系指出，本文遵守CC 4.0 BY-SA版权协议，转载请联系作者并注明出处，谢谢。

联系方式：

e-mail: FesianXu@gmail.com

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

微信公众号：机器学习杂货铺3号店

AUC曲线下面积

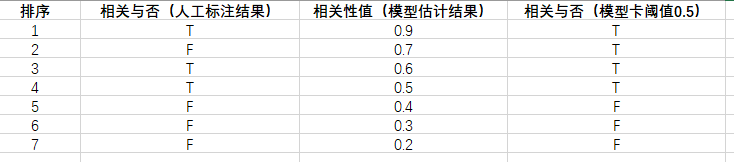
在搜索系统中，我们面对的需求可以简单描述为：用户给定一个检索词Query，然后系统返回一系列的文档doc，要求这些文档根据与Query的相关性进行降序排序，也即是相关性从高到低排序（根据相关性排序是检索系统最为基础的需求，商用检索系统中还会考虑很多其他因素，如doc的时效性，质量甚至是产品的定义等等）。对于每一个doc而言，会计算<Query-Doc>对的打分，范围区间假设为[0，1]。考虑到数据标注过程中，人类标注者很难对连续的相关性进行标注，因此通常只能离散地打标签，比如将相关性分为五档，最简单的就是二分类，相关或者不相关。因此，我们通常还是需要设置一个阈值，超过这个阈值的相关性我们认为是相关，反之是不相干。这个阈值的取值显然是。对于一个排序，如Fig 1.1所示，我们可以对于模型的打分设置一个阈值，认为的都是相关的，而反之不相干，假设，那么可以得到最后一列的相关与否（模型卡阈值0.5） 的结果。显然，这个结果和真实标注结果有一定差距。

Fig 1.1 对于一个排序而言，基于模型的相关性打分进行排序，而真实的相关与否是由人类专家评估的。

我们期望模型具有区分相关与否的能力，这是一种二分类的能力，衡量二分类的效果，我们可以用ROC（receiver operating characteristic）曲线进行评价，该曲线的横纵坐标分别是假阳性（False Positive Rate,FPR）和真阳性（True Positive Rate,TPR），这两个值的计算如公式(1.1)所示。

Fig 1.2 ROC曲线，该曲线描述了一个二分类系统的综合性能。

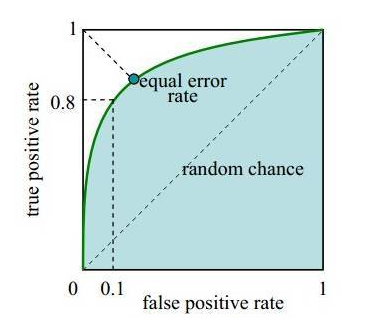
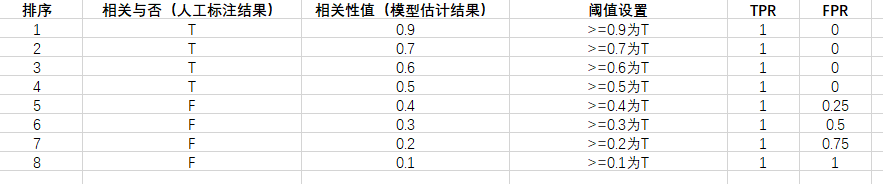
TPR表示将正例分对的概率，FPR表示将负类错分为正例的概率。通过遍历设置不同可能的阈值，我们可以计算出不同的TPR和FPR，并在ROC曲线上绘制出来，最后可以连成一条曲线，而其曲线下面积就是AUC指标了。假如我们的模型足够好，能够把所有相关的doc排到前面，那么有：

Fig 1.3 完美的排序结果，将所有相关的都排到了前面，其TPR都是1.0，ROC为经过左上角顶点的曲线。

该ROC曲线此时为：

Fig 1.4 完美情况下的ROC曲线，经过左上角顶点。

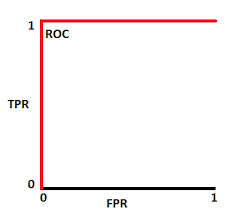
因此AUC范围在，其中在区间的才是有效的模型（当然，如果能够一直保持反预测，也是有效的模型）。其他关于ROC曲线的计算可见[1]。

累计增益（CG）

累计增益（cumulative gain，CG），该指标只是对前K个检索结果的相关性进行累加而已，没有考虑到特定位置的排序因素，公式为：其中的为第个位置的相关性程度（当然，是真实的ground truth，可以是五档相关性，也可以是0/1相关性）。显然这种太过于粗糙，没有考虑到排序不同位置的相关性造成的影响。

折损累计增益（DCG）

折损累积增益（Discount Cumulative Gain,DCG）在每一个CG的结果基础上考虑到了位置排序的关系，直观来看，越靠前的doc如果真实的相关性越强，那么给予的奖励也越多，而相对应的排得靠后的doc即便真实的相关性强，也需要加以惩罚。可以用公式(3.1)进行计算，其中的系数就是考虑到了第位置的排序影响，越后的排序，影响力越小。如果是二值的相关性，那么工业界上还会用式子(3.2)计算DCG：

NDCG

归一化折损累计增益（Normalized DCG），因为不同的Query其检索结果数量都可能不同，而DCG是简单的累加，使得不同Query之间的检索结果质量难以通过DCG进行对比，NDCG考虑进行归一化处理，其方法就是通过一个归一化系数：其中的是在第个位置时，理想排序情况下的最佳值，计算如：其中的表示，将所有doc的真实相关性降序排序，然后取前个结果组成的集合。也就是按照最优的方式对结果进行排序。

实际的例子 来源于[2]：

假设搜索回来的5个结果，其真实的相关性分数分别是 3、2、3、0、1、2。那么 CG = 3+2+3+0+1+2，可以看到只是对相关的分数进行了一个关联的打分，并没有召回的所在位置对排序结果评分对影响。而我们看DCG：

i	reli	log2(i+1)	reli /log2(i+1)
1	3	1	3
2	2	1.58	1.26
3	3	2	1.5
4	0	2.32	0
5	1	2.58	0.38
6	2	2.8	0.71

所以 DCG = 3+1.26+1.5+0+0.38+0.71 = 6.86，接下来我们归一化，归一化需要先结算 IDCG，假如我们实际召回了8个物品，除了上面的6个，还有两个结果，假设第7个相关性为3，第8个相关性为0。那么在理想情况下的相关性分数排序应该是：3、3、3、2、2、1、0、0。计算IDCG@6:

i	reli	log2(i+1)	reli /log2(i+1)
1	3	1	3
2	3	1.58	1.89
3	3	2	1.5
4	2	2.32	0.86
5	2	2.58	0.77
6	1	2.8	0.35

所以IDCG = 3+1.89+1.5+0.86+0.77+0.35 = 8.37，最终 NDCG@6 = 6.86/8.37 = 81.96%。

PAIR正逆序比

正逆序比 （Pair）也是对检索性能进行衡量的常用指标。首先我们需要知道什么是正序对，如果对于一个Query，有一个doc排序，其中的表示其中的排序位置，对于真实排序而言，我们知道，当时，，其中表示真实排序的相关性打分。假如根据我们的模型相关性打分也可以排列出一个doc排序，对于给定的，如果有的同时，其中是模型预测的相关性得分，我们称之为正序对，反之则为逆序对。我们举个例子，假如根据真实人工标记的相关性，有排序[1,3,4,6]，其中的数字表示doc的id编号，那么如果我们的模型排序为[1,4,6,3]，那么此时对于真实排序的<3,4>而言，预测模型的<4,3>就是逆序对，而对于真实排序的<1,6>而言，预测模型的<1,6>就是正序对，而正逆序比就是正序对的数量比上逆序对的数量，这个指标表示了排序的有序性，越大越好，值域为。 $正序对逆序对$

mAP

这个指标我们经常见到，之前在[3]中曾经介绍过在Object Detection任务中的mAP定义，在检索系统中，mAP的定义也是类似的。首先我们要知道什么是AP（Average Precise），对于一个排序任务而言，会根据模型预测的得分进行降序，如Fig 1.1所示，排在前面的结果不一定就完全是相关的，排在后面的结果不一定完全不相关，为了衡量模型预测的准确性，我们对前个结果进行精准率的计算[1]，得到，对于前个逐个计算，然后求平均就得到了AP: 对于所有的查询的AP进行求平均，就得到了mAP：

Reference

[1]. https://blog.csdn.net/LoseInVain/article/details/78109029

[2]. https://www.cnblogs.com/by-dream/p/9403984.html

[3]. https://blog.csdn.net/LoseInVain/article/details/106442683