在立体视觉中,对单应性矩阵进行估计是一个很重要的任务,我们在之前的博文[1,2,3]中的讨论中都或多或少地涉及到了单应性矩阵,我们知道它是在投影变换中保持共线性的一种性质。在本文中,我们将讨论如何通过匹配点的关系,对单应性矩阵进行估计。
前言
在立体视觉中,对单应性矩阵进行估计是一个很重要的任务,我们在之前的博文[1,2,3]中的讨论中都或多或少地涉及到了单应性矩阵,我们知道它是在投影变换中保持共线性的一种性质。在本文中,我们将讨论如何通过匹配点的关系,对单应性矩阵进行估计。如有谬误,请联系指出,转载请联系作者并注明出处,谢谢。
注:本文参考[7]的内容。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号:机器学习杂货铺3号店

估计问题
估计(estimation)是什么?这个词我们在统计学中经常听到,估计指的是基于观测数据的基础上,对一个模型的参数进行估计,在立体视觉中,一般有以下几种估计问题:
- 2D 单应性(2D homography): 给定一系列点
,并且给定其对应的匹配点 ,我们的估计的目标是根据这些对应点,估计出能够将 的投影变换。在实际中, 和 通常是两张不同的图片上的对应/匹配点(match points),每个图片都可以看成是投影空间 。在本路问题中,其实就是根据2D匹配点进行单应性矩阵 的估计。 - 3D到2D的相机投影(3D to 2D camera projection):给定在三维空间中的点
,并且给定这些3D点在平面图像上的对应的2D点 。在这里的估计指的就是估计这里的3D到2D的投影变换 ,这里的投影通常是由投影相机模型得到的,参考[4]的讨论内容。 - 基础矩阵的计算(Fundamental matrix computation):给定在一张图像上的一系列点
和其在另一张图像上的对应点集 ,计算根据这些对应关系计算出来的基础矩阵,我们在[5]中介绍过本征矩阵和基础矩阵,我们知道基础矩阵 是一个对所有的 都满足 的 的矩阵。 - 三焦张量计算(Trifocal tensor computation): 给定三张图片中的对应关系:
,计算其三焦张量(Trifocal tensor), 三焦张量对三张图像的对应点或者对应线进行了关系联系。
这些问题都是考虑到了“对应性”(correspondance),或者说是“匹配性”,然后对某种变换进行参数估计,因此这四个问题或多或少有着关联。在此,我们仅讨论第一种问题,其中提出的解法,能对其他三种问题的解决提供思路。
估计单应性矩阵
重申下问题:
我们考虑两个图像之间的匹配点集
,我们需要估计出单应性矩阵 ,使得对于所有的 都有 。
首先我们需要确定至少需要多少对匹配点集才足以确定一个单应性矩阵,我们知道单应性矩阵有9个元素,但是其可以进行尺度归一化[6],因此2D的单应性矩阵只有8个自由度(同理,3D的单应性矩阵为15的自由度)。每一对匹配点集提供了两个自由度的约束(也就是x和y),因此最少需要四对匹配点集才足以确定一个单应性矩阵。
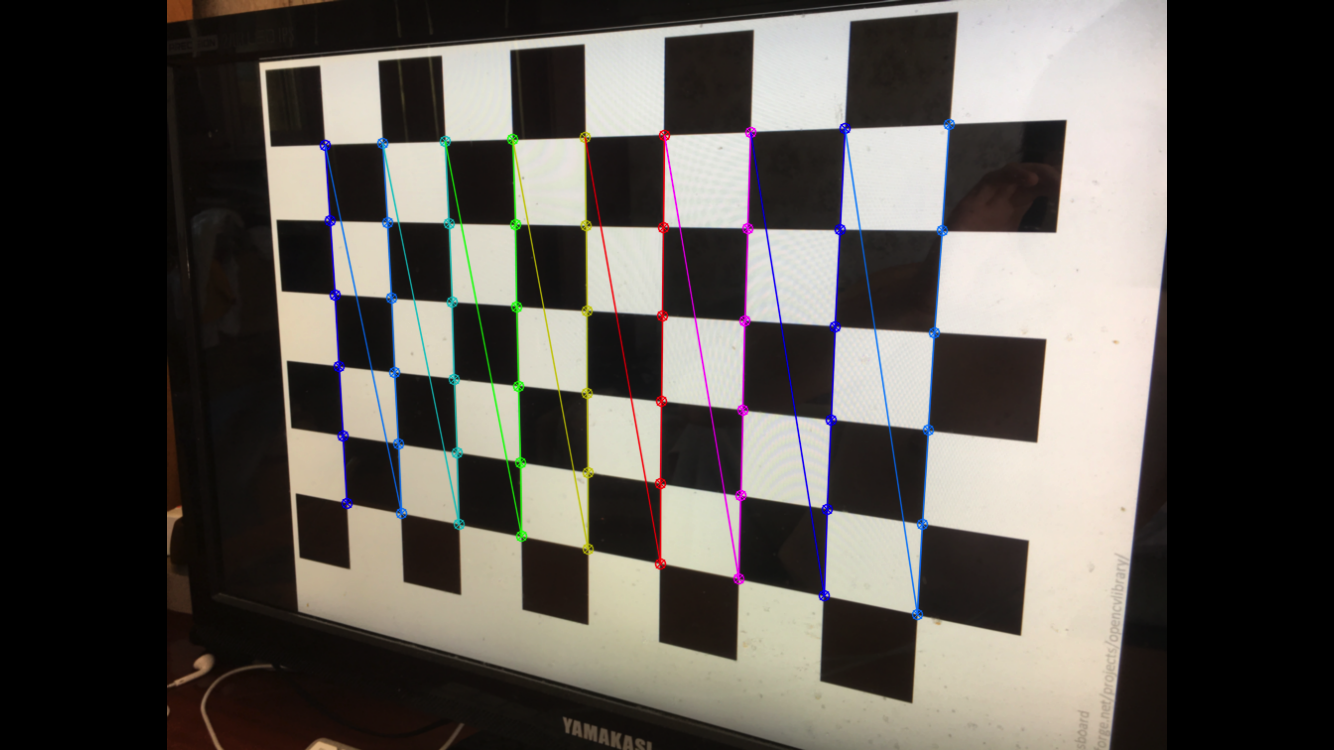
自然地,给定了4对匹配点集(其中不能是三点共线的,我们后续讨论),我们可以确定一个单应性矩阵,这个是最小解。然而在实际中,我们通常能得到两张图片的很多对匹配点集,如Fig 1.1所示,而通常在这很多的匹配点集中,存在有误匹配的情况,这些误匹配称之为噪声(noise),通常我们会采用类似于RANSAC的鲁棒估计减少噪声的干扰(我们将在以后的博文中讨论RANSAC鲁棒估计)。除了鲁棒估计,我们也可以通过设置一个损失函数(cost function),尝试最小化损失函数,我们能找到一个最佳的单应性矩阵估计。一般来说,有两大类的损失函数:
- 基于代数损失的(algebraic error),也就是不考虑图像的几何上的因素,只考虑代数形式上的损失。
- 基于几何损失(geometric error)或统计上的图像距离的(statistical image distance),这种损失函数通常带有图像几何上的意义。

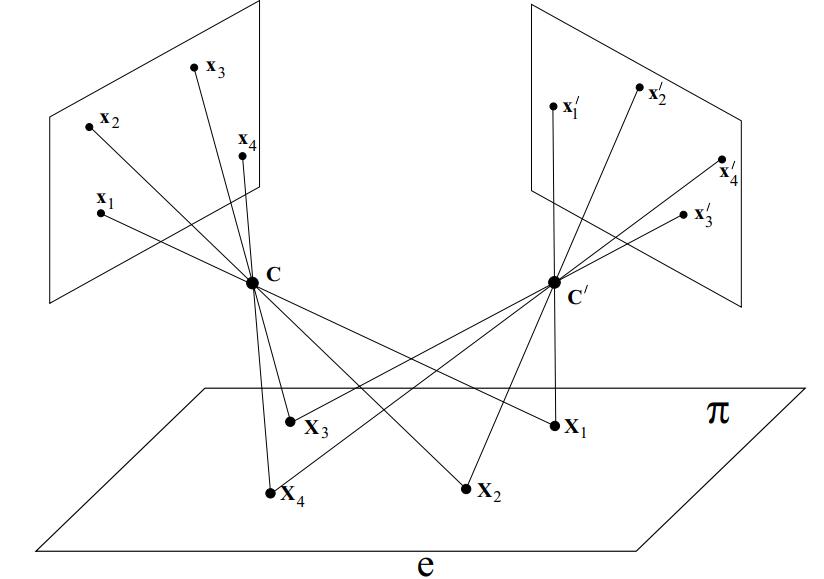
通常在对同一个平面上的点进行多视角摄像时,如Fig 1.2,图像中的像素点可以视为是投影变换的,可以用单应性矩阵对应,在进行弱透视摄像时[9],同样也可以这样认为。
DLT算法
我们首先考虑一个简单的线性算法。在给定了4对2D到2D的匹配点集时
又因为这个表示是在齐次坐标系下的,我们可以让
当给出超过4对匹配点的时候,我们处在超定方程(over-determined)的情况,此时可能没有一个解可以精确地满足所有点的匹配关系,因此我们设计一个损失函数,让损失函数最小以达到最佳的估计效果。因为我们知道
其他的损失函数
代数距离
代数距离(algebraic distance),我们在(1.7)中尝试去最小化的
几何距离
在讨论几何距离之前,我们要明晰三种不同的概念:
在一张图像上的误差,迁移误差:
如果我们假设在第一张图像上,其测量到的点不存在误差,也就是说假设第一张图上有

考虑到这种假设合理的情况,我们设计出所谓的最小化 迁移误差(transfer error),公式表示如(1.11)所示
注意,这里的欧式距离
对称迁移误差:
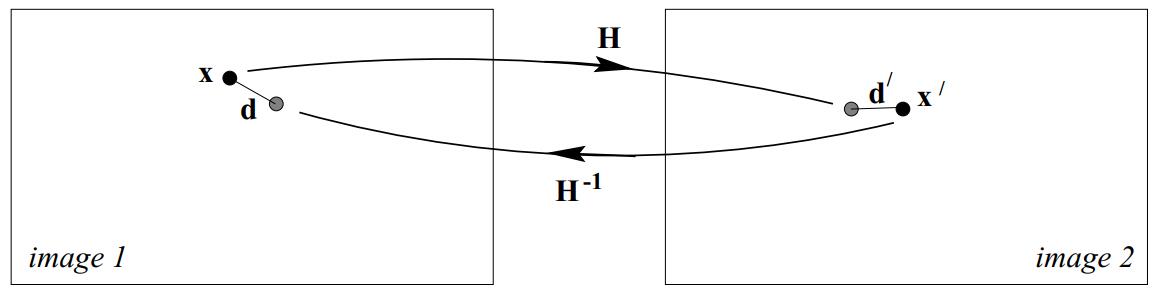
然而更为通用且实际的方法,是考虑所谓的对称迁移,也就是将第一张图像上的像点投射到第二张图像,计算误差
重投影误差:
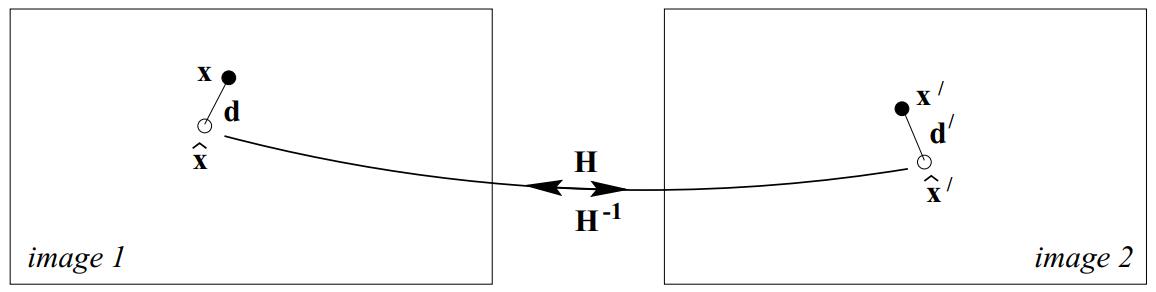
我们从式子(1.14)和Fig 1.5中发现,其实我们的投影点和实际点并不是完全匹配的,因为我们的观察点都是带噪声的,并不是实际理论上的完美的点,因此即便通过单应性矩阵它们也不会完全的重合。我们可以考虑一种这种情况,假设我们通过匹配点集
Reference
[1]. https://blog.csdn.net/LoseInVain/article/details/104533575
[2]. https://blog.csdn.net/LoseInVain/article/details/102739778
[3]. https://blog.csdn.net/LoseInVain/article/details/103369203
[4]. https://blog.csdn.net/LoseInVain/article/details/102632940
[5]. https://blog.csdn.net/LoseInVain/article/details/102665911
[6]. https://blog.csdn.net/LoseInVain/article/details/104533575
[7]. Hartley R, Zisserman A. Multiple view geometry in computer vision[M]. Cambridge university press, 2003.
[8]. https://blog.csdn.net/LoseInVain/article/details/102756630
[9]. https://blog.csdn.net/LoseInVain/article/details/102883243
[10]. https://blog.csdn.net/LoseInVain/article/details/102739778
[11]. https://blog.csdn.net/LoseInVain/article/details/102632940