在上一篇文章中[1]，我们介绍了Graph Convolution Network的推导以及背后的思路等，但是，其实我们会发现，在傅立叶域上定义出来的GCN操作，其实也可以在空间域上进行理解，其就是所谓的消息传递机制，我们在本篇文章将会接着[1]，继续介绍Message Passing机制。

FesianXu 5/20, 2019 at UESTC

前言

在上一篇文章中[1]，我们介绍了Graph Convolution Network的推导以及背后的思路等，但是，其实我们会发现，在傅立叶域上定义出来的GCN操作，其实也可以在空间域上进行理解，其就是所谓的消息传递机制，我们在本篇文章将会接着[1]，继续介绍Message Passing机制。如有谬误请联系指出，本文遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明并且联系笔者，谢谢。

联系方式：

e-mail: FesianXu@gmail.com

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

微信公众号：机器学习杂货铺3号店

Message Passing与GCN

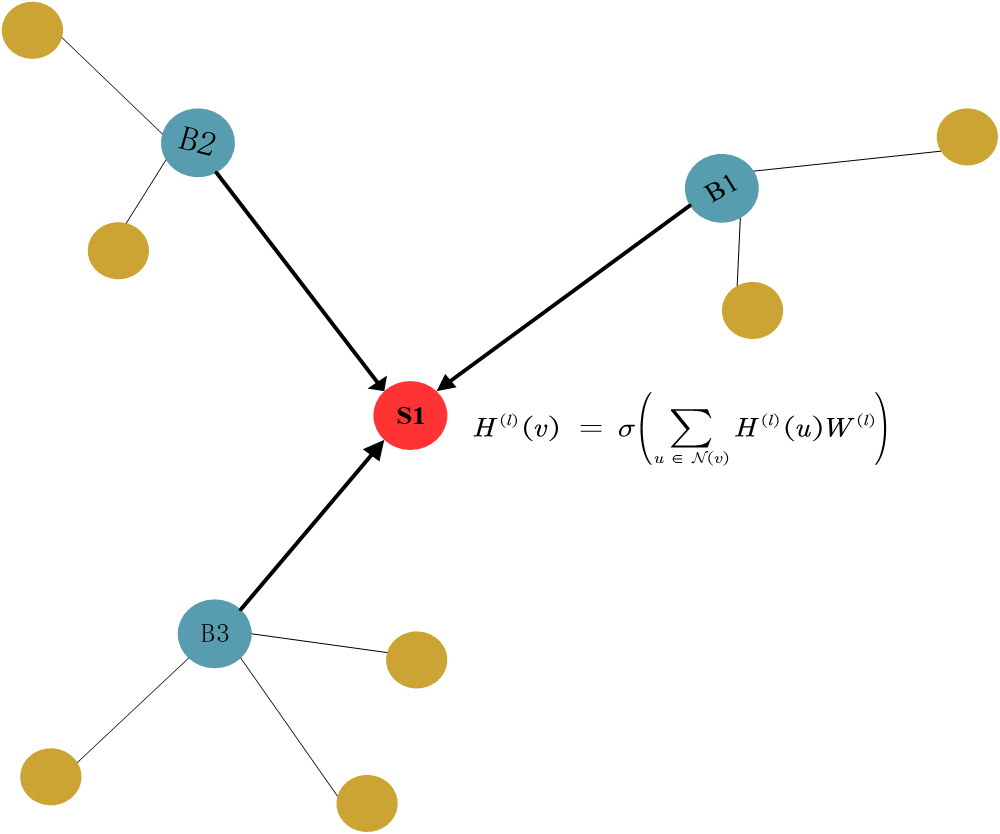
消息传递(Message Passing) 正如其名，指的是目的节点的邻居，如Fig 1所示，红色节点的邻居正是蓝色节点，这些邻居节点根据一定的规则将信息，也就是特征，汇总到红色节点上，就是所谓的信息传递了。让我们举个信息汇聚的最简单的例子，那就是逐个元素相加。假设我们的每个节点的特征为，那么有：其中，表示的是节点的邻居节点。

Fig 1. 关于消息传递的一个例子其中蓝色节点是红色节点的一阶直接邻居。

通常来说，我们会加入一个线性变换矩阵，以作为汇聚节点特征的特征维度转换（或者说是映射）。有：加入激活函数后有: 其实式子(1.3)可以用更为紧致的矩阵形式表达，为：其中为邻接矩阵，接下来我们以Fig 2的拓扑结构举个例子进行理解。

Fig 2. 一个图的拓扑结构例子，其中D是度数矩阵，A是邻接矩阵，L是拉普拉斯矩阵。

此时假设我们的输入特征为10维，输出特征为20维，那么我们有：那么进行运算的过程如：

Fig 3. 输出矩阵的行表示节点，列表示特征维度。

Fig 4. 邻接矩阵乘上特征矩阵，相当于进行邻居节点选择。

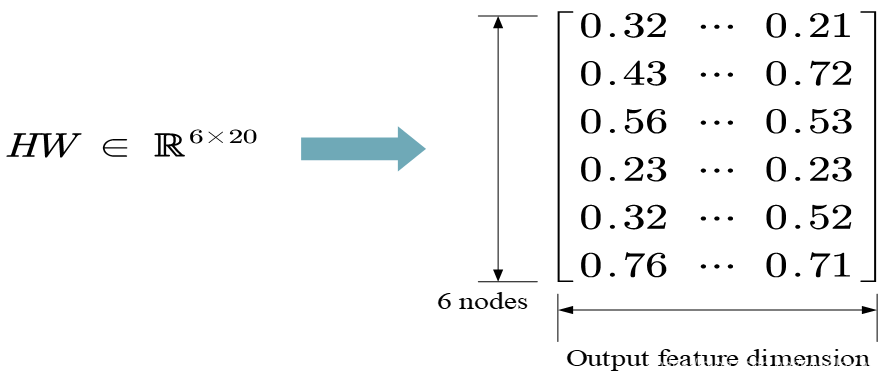
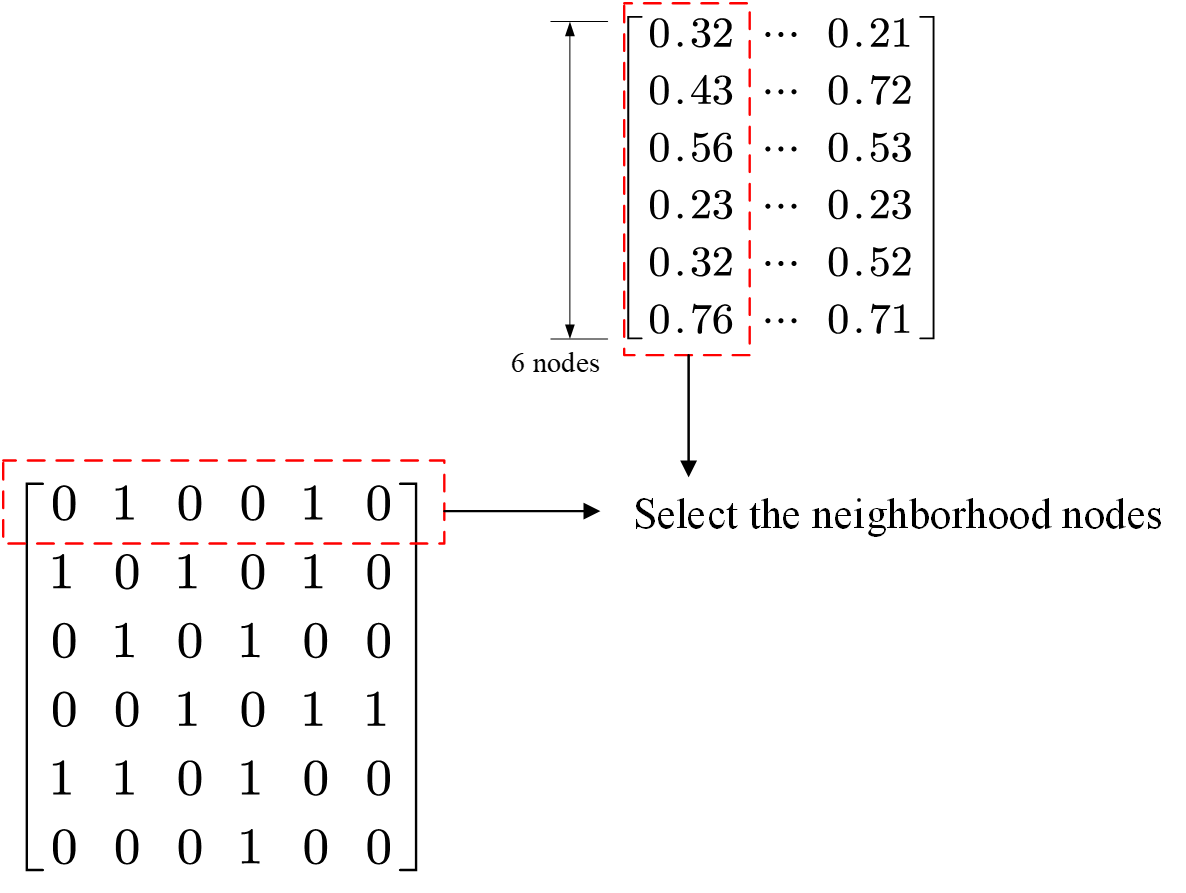
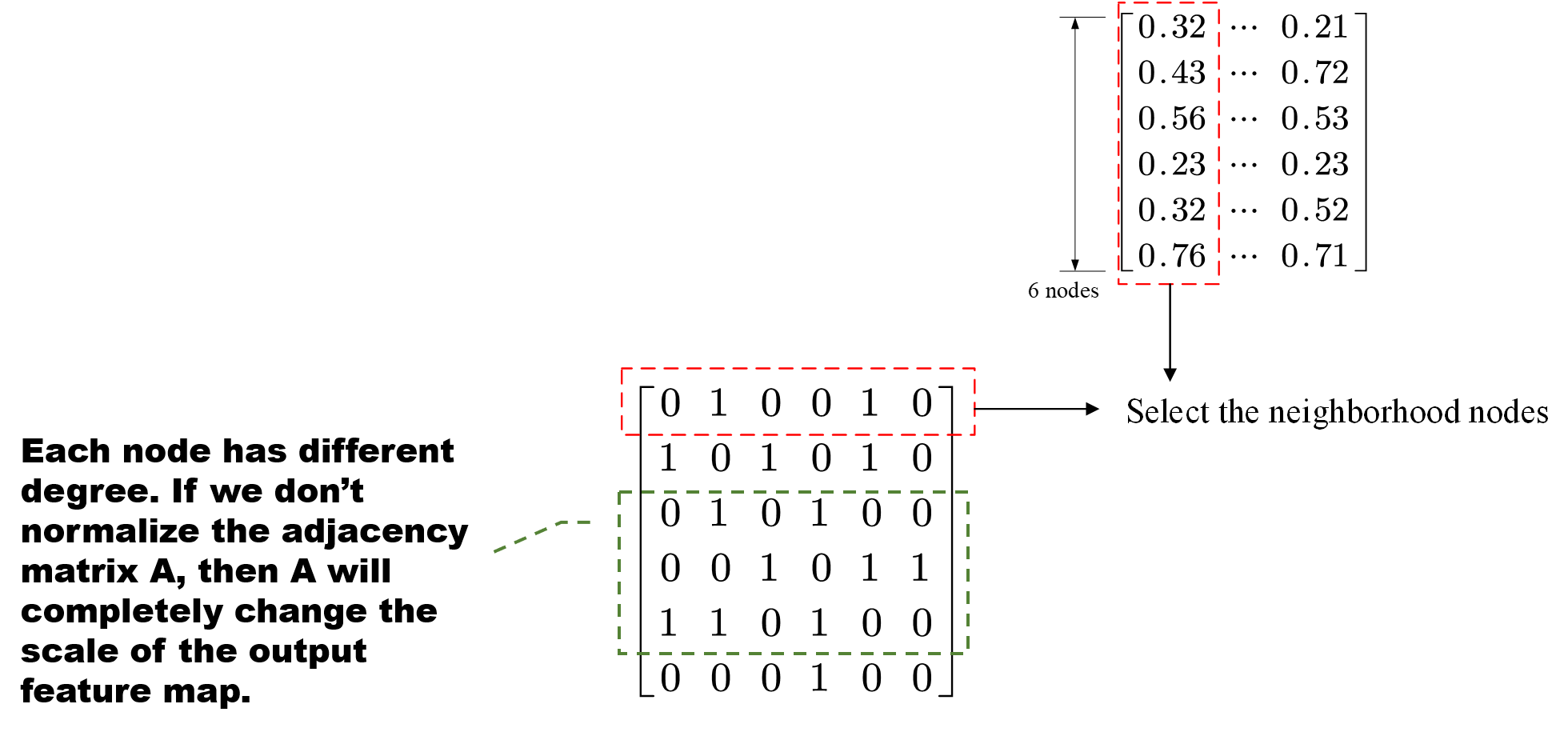
我们不难发现，其实的结果乘上邻接矩阵的目的其实在于选在邻居节点，其实本质就是在于邻居节点的信息传递。因此信息传递的公式可以用更为紧致的式子(1.4)进行描述。但是我们注意到，如Fig 5的绿色框所示的，每一行的节点总数不同，将会导致每个目的节点汇聚的信息尺度不同，容易造成数值尺度不统一的问题，因此实际计算中常常需要用标准化进行处理，这正是[1]中提到的对拉普拉斯矩阵进行标准化的原因。

Fig 5. 注意绿色框，其每一行的节点总数不同会导致数值不统一尺度的问题。

除了标准化的问题之外，式子(1.4)还存在一些需要改进的地方，比如没有引入节点自身的信息，一般来说，比如二维卷积，像素中心往往能提供一定的信息量，没有理由不考虑中心节点自身的信息量，因此一般我们会用自连接将节点自身连接起来，如Fig 6所示。

Fig 6. 引入节点自身的信息。

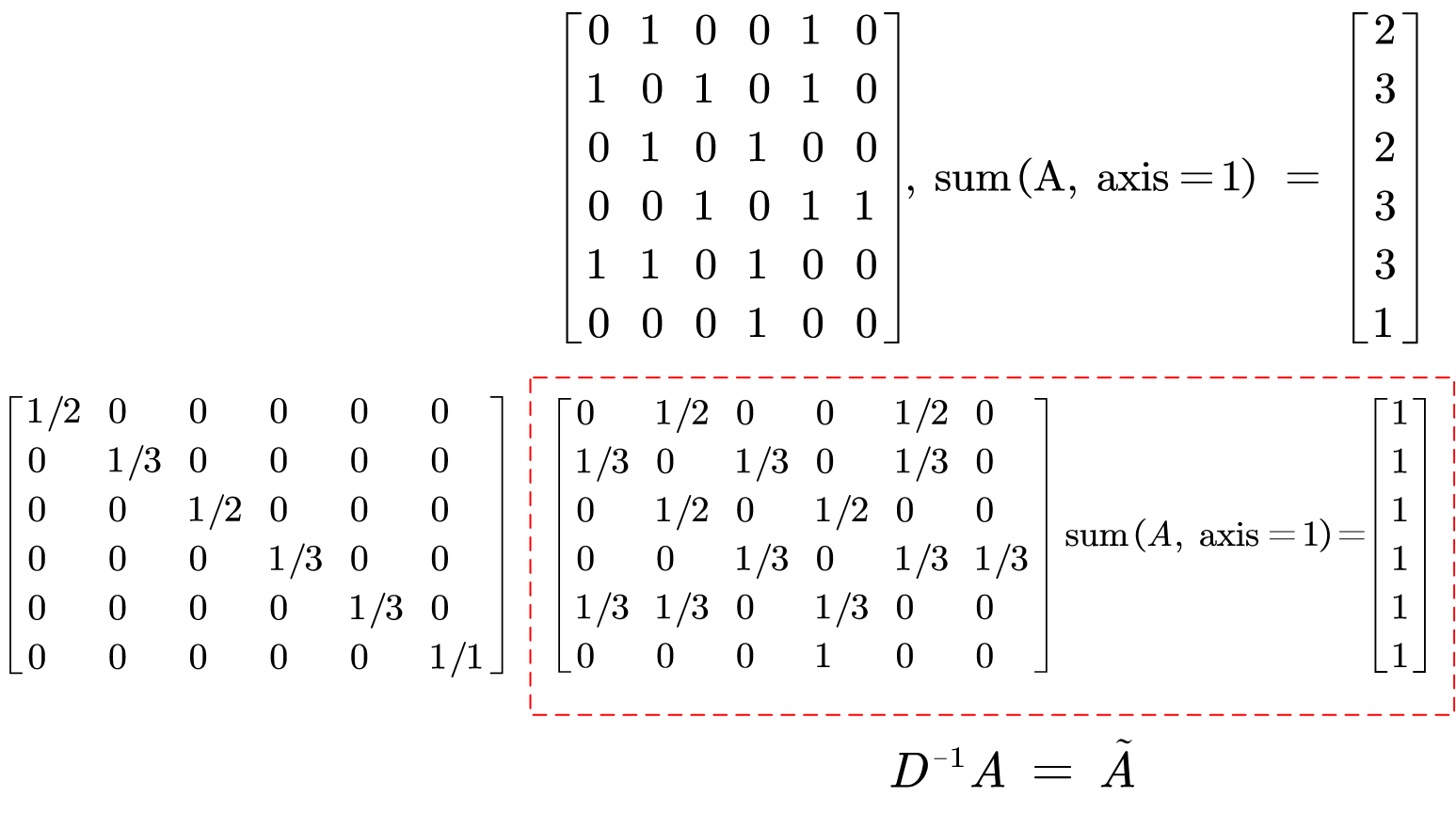
因此，邻接矩阵就应该更新为: 而度数矩阵更新为：为了标准化邻接矩阵使得每行之和为1，我们可以令：也就是邻居节点的特征取平均，这里对这个过程同样制作了个详细解释的图。

Fig 7. 进行标准化，使得不受节点度数不同的影响。

我们可以看到，通过式子(1.7)，我们对邻接矩阵进行了标准化，这个标准化称之为random walk normalization。然而，在实际中，动态特性更为重要，因此经常使用的是symmetric normalization [2,3]，其不仅仅是对邻居节点的特征进行平均了，公式如：同样，这里我制作了一个运算过程图来解释。

Fig 8. 对称标准化示意图。其中的axis=0应该修正成axis=1，源文件丢失了，暂时没空重新制图。

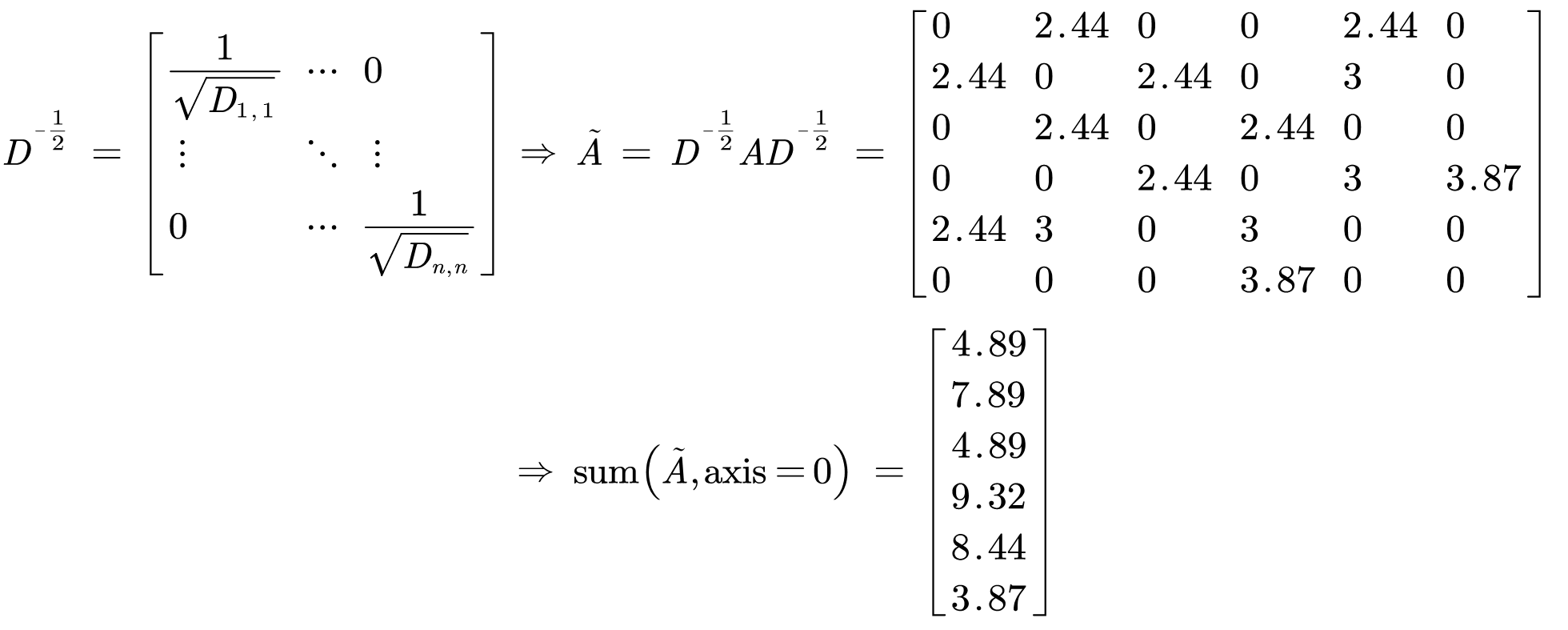
对拉普拉斯矩阵进行对称标准化，有：这就是为什么在[1]中提到的拉普拉斯矩阵要这样标准化的原因了。

所以，经过了对称标准化之后，我们的式子(1.4)可以写成：其中熟悉吧，这个正是根据频域上ChebNet一阶近似得到的结果来的GCN表达式，因此GCN在空间域上的解释就是Message Passing。

该系列的其他文章

Reference

[1]. https://blog.csdn.net/LoseInVain/article/details/90171863

[2]. https://people.orie.cornell.edu/dpw/orie6334/lecture7.pdf

[3]. https://math.stackexchange.com/questions/1113467/why-laplacian-matrix-need-normalization-and-how-come-the-sqrt-of-degree-matrix