我们曾在[1]中探讨了欧几里德结构数据(如图像,音视频,文本等)和非欧几里德结构数据(如Graph和Manifold等)之间的不同点,在本文中,我们探讨如何在非欧几里德结构数据,特别是Graph数据上定义出卷积操作,以便于实现深度神经学习。
前言
我们曾在[1]中探讨了欧几里德结构数据(如图像,音视频,文本等)和非欧几里德结构数据(如Graph和Manifold等)之间的不同点,在本文中,我们探讨如何在非欧几里德结构数据,特别是Graph数据上定义出卷积操作,以便于实现深度神经学习。如有谬误请联系指出,本文遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明并且联系笔者,谢谢。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号: 机器学习杂货铺3号店

非欧几里德数据 嵌入 欧几里德空间
我们提到过欧几里德数据可以很容易嵌入到欧几里德空间中,无论是样本空间还是经过特征提取后的特征空间,这个特性可以方便后续的分类器设计。然后,遗憾的是,非欧几里德数据因为天然地具有不固定的领域元素数量或者连接数量等,不能直观地嵌入欧几里德空间,并且也很难在Spatial上定义出卷积操作出来,而这个卷积操作,在欧几里德数据上是很直观可以定义出来的,如:
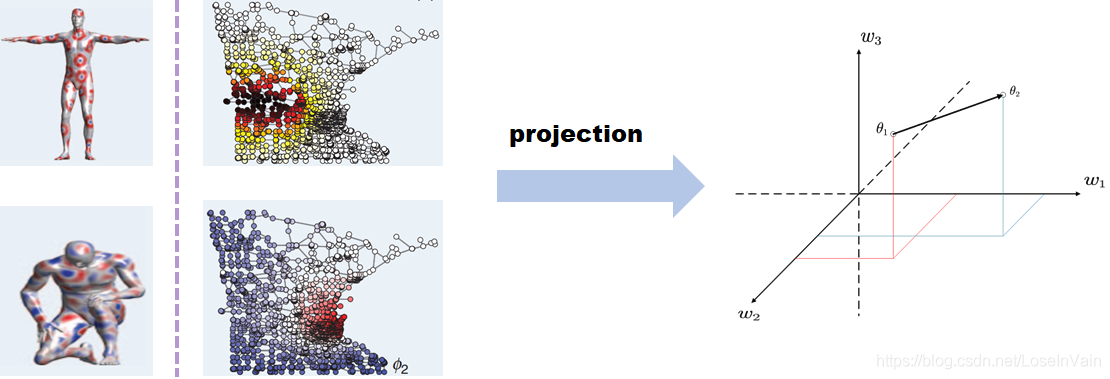
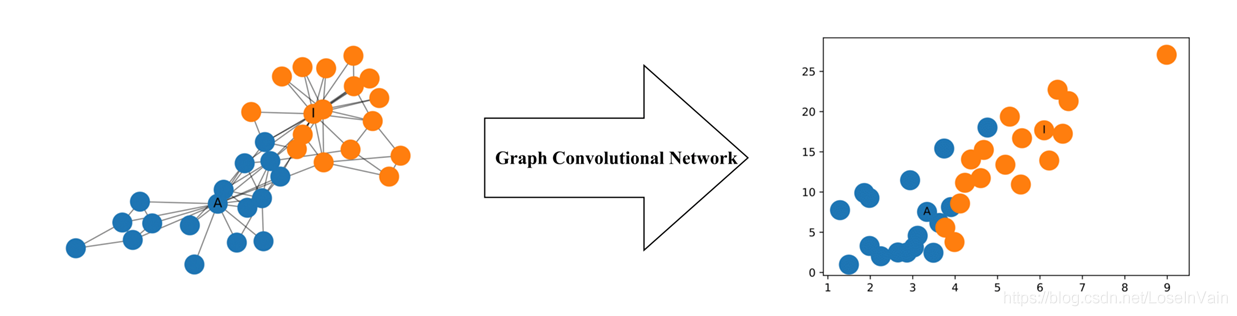
有了这个操作,即便是对于元素排列不整齐的Graph或者Manifold,也可在欧几里德空间进行样本之间的距离度量了,而且,这个过程还往往伴随着降维,减少计算量,方便可视化等优点。这个将会方便后续的分类器,聚类器等设计。
Graph Deep Learning
因为Graph数据是最为常见的非欧几里德数据,我们这里以图深度学习为例子。图深度学习的任务目标可以分为几种:
- 将有着不同拓扑结构,不同特征的图分类为几类。在这种情况是对整个Graph进行分类,每个Graph有一个标签。
- 对一个Graph的所有节点node进行分类。这种情况相当于是文献引用网络中对文献类型分类,社交网络对用户属性分类,每个节点有一个标签。
- 生成一个新的Graph。这个相当于是药物分子的生成等。
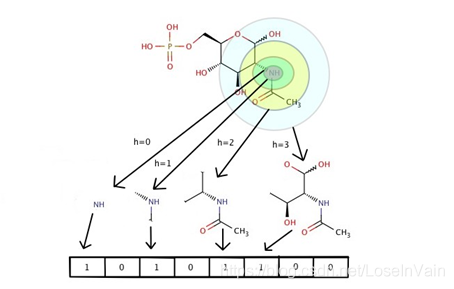
其中,最为常见的是第一类型,我们对此进行详细的任务定义如:
我们用
表示一个图,其中 是对于图的邻接矩阵[2],而 是节点的特征矩阵,其中 表示有n个节点,d表示每个节点有d个特征。给定一个有标签的graph样本集: ,其中 是标签有限集合,并且对应于 ,那么我们的学习目标就是学习到一个映射 使得:
在频域定义卷积
我们之前谈到在spatial域上难以直接定义graph的卷积操作,那么我们自然就想到如果能在频域定义出来卷积,那也是不错的,因此我们接下来想要探讨怎么在频域定义卷积。在此之前,我们需要了解下热传播模型的一点东西,因为图中节点的信息传递,一般来说是通过邻居节点进行传递的,这一点和物体将热量从高到低的传递非常相似,可以对此建立和热传递相似的模型。
在[3]的这篇回答中,作者对热传播和图节点信息传递进行了非常精彩的阐述,并且引出了 拉普拉斯矩阵(Laplacian Matrix) 对于节点之间关系的描述作用,值得各位读者参考。
总的来说,就是对拉普拉斯矩阵进行特征值分解,其每个特征向量可以看成是频域中正交的正交基底,其对应的特征值可以看成是频率,对拉普拉斯矩阵进行特征值分解的公式如下:

总的来说,用拉普拉斯矩阵可以在某种程度上表示一个Graph的拓扑结构,这点和邻接矩阵相似。
注意到我们有对拉普拉斯矩阵
那么对于一个卷积核
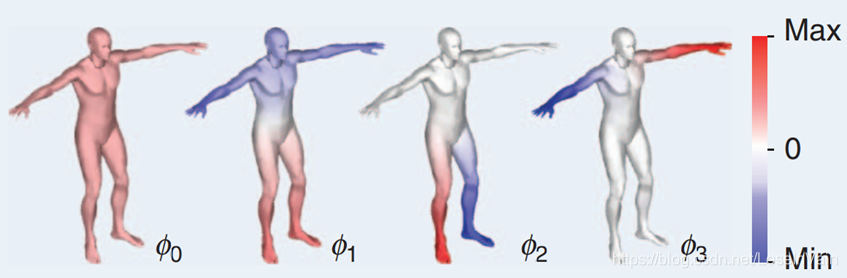
类似于一般欧几里德结构数据的傅立叶变换,在图傅立叶变换中,其每个基底(也就是特征向量)也可以可视化出来,如Fig 4所示:

ChebNet, 切比雪夫网络
上面介绍的网络有两个很大的问题:
- 它们不是在空间上具有局部性的,比如二维图像的卷积网络就具有局部性,也称之为局部连接,某个输出神经元只是和局部的输入神经元直接相连接。这个操作有利于减少计算量,参数量和提高泛化能力。
- 计算复杂度为
为了解决第一个问题,我们把
若节点
和节点 的最短路径 ,那么有 ,其中 为拉普拉斯矩阵。
因此有:
注意到,在式子
一种解决方法就是把
因此,最后对于第
ChebNet一阶近似
根据我们之前的讨论,K阶的ChebNet可以表示为:
另外,为了增加节点自身的连接(这个我们以后继续讲解),我们通常会对邻接矩阵
本篇文章就此结束,我们在下一篇文章将会继续介绍GCN在空间域上的理解,即是基于消息传递(Message Passing)中的解释,并且会举出一些例子来方便理解。
该系列其他文章
- 《学习geometric deep learning笔记系列》第一篇,Non-Euclidean Structure Data之我见
- 《Geometric Deep Learning学习笔记》第三篇,GCN的空间域理解,Message Passing以及其含义
Reference
[1]. https://blog.csdn.net/LoseInVain/article/details/88373506
[2]. https://en.wikipedia.org/wiki/Adjacency_matrix
[3]. https://www.zhihu.com/question/54504471/answer/630639025
[4]. https://blog.csdn.net/wang15061955806/article/details/50902351
[5]. Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[C]//Advances in neural information processing systems. 2016: 3844-3852.
[6]. Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[J]. arXiv preprint arXiv:1409.1556, 2014.
[7]. Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.