最近笔者看论文[1]的时候发现有个术语local affine transformation,也就是所谓的局部仿射变换,仿射变换笔者之前有过研究[2],还算是比较清楚,但是谈到什么是“局部”仿射变换,就没有头绪了。后面笔者查找资料[3]后,终于有所了解,因此简要笔记与此,希望对大家有所帮助。
前言
最近笔者看论文[1]的时候发现有个术语local affine transformation,也就是所谓的局部仿射变换,仿射变换笔者之前有过研究[2],还算是比较清楚,但是谈到什么是“局部”仿射变换,就没有头绪了。后面笔者查找资料[3]后,终于有所了解,因此简要笔记与此,希望对大家有所帮助。如有谬误,请联系指出,转载请联系作者并注明出处。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号:机器学习杂货铺3号店

注意:本文为了描述局部仿射变换的应用场景,会介绍一下手写字符匹配,如果需要快速了解局部仿射变换,请直接跳到最后两章。
回顾仿射变换
我们之前在博文[2,4]中谈到过仿射变换,简单来说就是仿射变换是几何图形之间保持平行线,共线性的一种线性变换,在二维情况下,我们用齐次坐标系[4]可以表示为:
手写字符匹配
在说到局部仿射变换之前,我们先提一下手写字符匹配这个应用场景,在这个场景里面,局部仿射变换有着其作用之地。对于某个手写字符,比如“大”字,我们可以设置一个标准的参考字符,我们分别用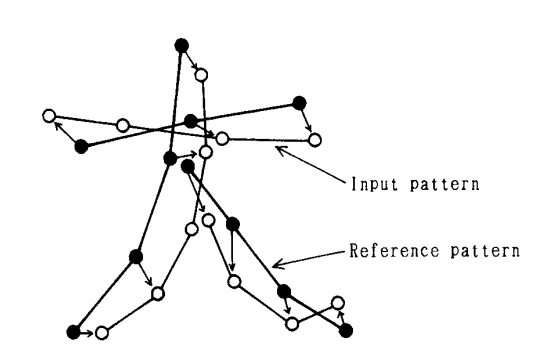
注意到一种现象,在式子(2.3)中其实考虑的是每个点之间的匹配关系,我们称之为全局匹配关系,而在手写字体和参考字体的真实匹配过程中,其实可能存在局部的匹配关系,即是某些部分的匹配比较接近,而某些部分的匹配不够接近,如果把这两个结果一起优化(即是全局),则优化过程可能对局部优化较好的结果产生不好的影响。为了避免全局信息对局部信息产生影响,此时需要考虑局部的匹配结果优化。
局部仿射变换
我们假设输入的字符特征点可以用参考字符特征点的仿射变换表示,那么有:
可知对于
通过这个权重参数
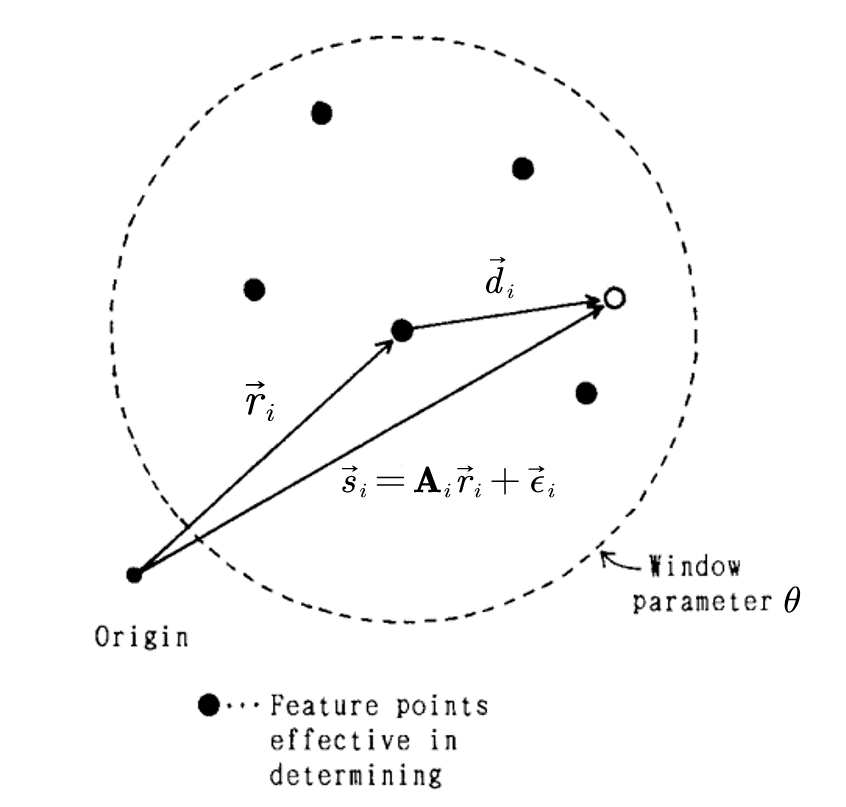
容易发现,当
总结
总结来说,全局仿射变换和局部仿射变换的区别在于,在局部仿射变换过程中,求解仿射变换矩阵的参考点是局部的,在对于某些存在局部变形的应用中,会更为适合用局部仿射变换去求解局部仿射变换矩阵。
Reference
[1]. Siarohin, A., Lathuilière, S., Tulyakov, S., Ricci, E., & Sebe, N. (2019). First order motion model for image animation. In Advances in Neural Information Processing Systems (pp. 7137-7147).
[2]. https://blog.csdn.net/LoseInVain/article/details/104533575
[3]. Wakahara, T. (1988, January). Online cursive script recognition using local affine transformation. In 9th International Conference on Pattern Recognition (pp. 1133-1134). IEEE Computer Society.
[4]. https://blog.csdn.net/LoseInVain/article/details/102756630
[5]. https://blog.csdn.net/LoseInVain/article/details/80339201