我们知道在透视法中，相互平行的平行线会在无限远处相交于一点，我们称之为理想点（ideal point），对于这个透视成像的介绍，我们在之前的文章[1,2,3]中都或多或少介绍过，同时还引入了齐次坐标系，以便于对投影变换下的不同情况进行统一建模...

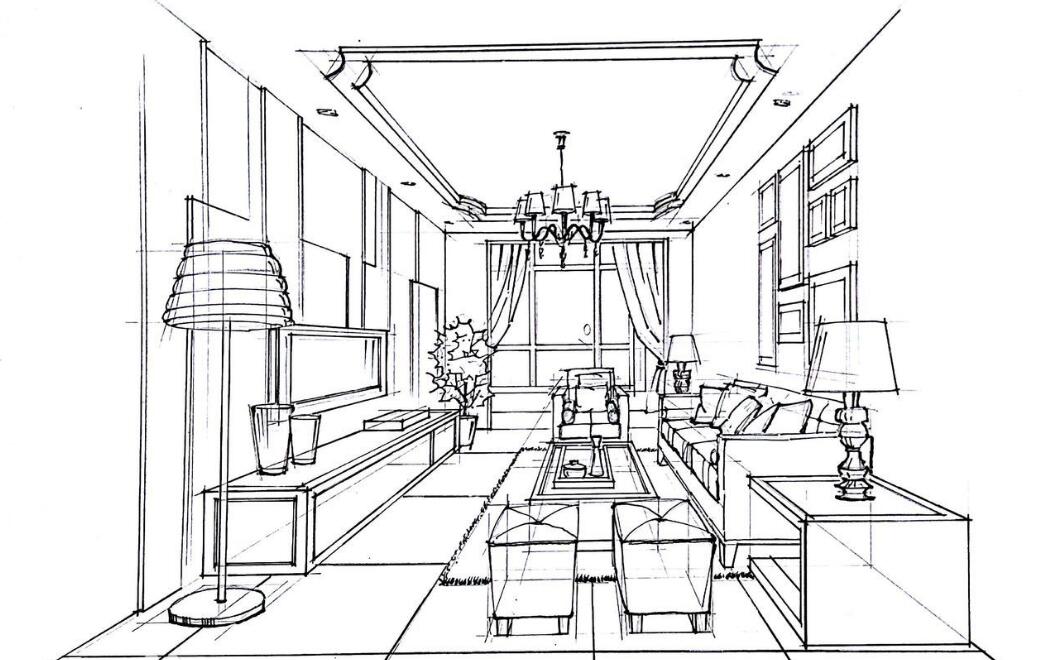
FesianXu 20210625 at Baidu search team

我们知道在透视法中，相互平行的平行线会在无限远处相交于一点，我们称之为理想点（ideal point），对于这个透视成像的介绍，我们在之前的文章[1,2,3]中都或多或少介绍过，同时还引入了齐次坐标系，以便于对投影变换下的不同情况进行统一建模。从直观上看，平行线在无限远处相交于一点的现象如Fig 1所示。透视现象也在工程制图，美术中有着诸多应用，如Fig 2所示。

Fig 1 足够长并且足够笔直的公路，在无限远处就会呈现汇聚于一点的趋势。

Fig 2 透视画法也是在美术，工程制图中经常使用技法，用于表示物体的三维空间中的立体信息，特别是深度信息。

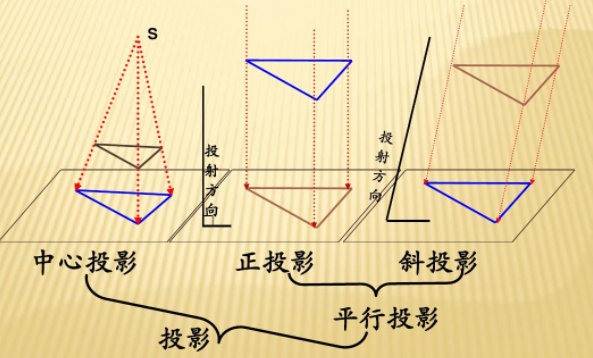
追本溯源而言，之所以会产生这种透视现象是中心投影 导致的，一般而言投影可以分为两种，分别是中心投影和平行投影，如Fig 3所示，其中中心投影的光线是发散的，由一个点发散得到；而平行投影的光线都是平行的。中心投影是目前相机针孔模型的理论模型[4]，人眼的成像也是可以视为是中心投影的，因此根据中心投影进行成像的图片具有和人眼成像相似的效果，也就是透视效果，呈现“近大远小”，也就更有立体感和真实感。而平行投影因为可以准确地描述客观物体的尺寸大小等属性，不会受到由于中心投影导致的尺度变换（包括其他投影变换，此处不展开讨论）影响等，因此在工程制图中广泛使用。

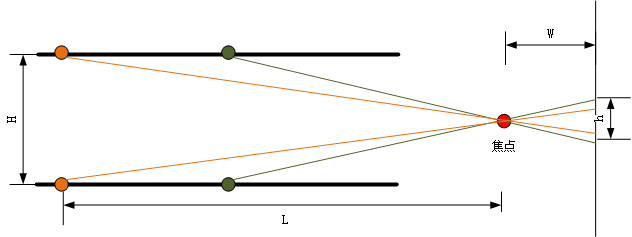
Fig 3 投影可分为中心投影和平行投影。而平行投影又可以分为正投影和斜投影。

在中心投影中，我们都知道会出现“近大远小”的现象，而出现这个现象的原因也很简单，正是由于真实世界中，物体距离相机（的焦点）有着不同距离导致的。以平行马路为例子，如Fig 4所示，假设黑色平行线的距离恒定是，而焦点到成像平面的距离固定是，那么距离焦点不同距离（体现在不同）的车道，如橘色点和绿色点所示的成像长度也不同。由简单的相似三角形原理可得：显然当车道在无穷远处时，有，即是: 也即是将会交于统一点。这也即是Fig 1中所呈现的效果。通过这个例子，我们明白了在中心投影情况下，由于现实物体的深度不同，将会导致一定的非线性“扭曲”，这种扭曲体现为投影变换，在特殊情况下就变成了透视现象。

Fig 4 图示解释为什么平行线在中心投影中，会趋向于会聚于无穷远处的一点。

Reference

[1]. https://fesian.blog.csdn.net/article/details/104533575

[2]. https://fesian.blog.csdn.net/article/details/102883243

[3]. https://fesian.blog.csdn.net/article/details/102756630

[4]. https://fesian.blog.csdn.net/article/details/102632940