在相机成像过程中,我们经常会提到相机的内参数,外参数,这些参数决定了一个相机的成像的效果,是后续一系列计算机视觉问题的基础中的基础,然而因为较为底层的原因,现在却比较少人关心它,笔者最近在学习一些底层的计算机视觉成像理论,感觉有所裨益,希望能在此进行笔记,作为备忘,如果能对读者有所帮助,则是更好不过了。
前言
在相机成像过程中,我们经常会提到相机的内参数,外参数,这些参数决定了一个相机的成像的效果,是后续一系列计算机视觉问题的基础中的基础,然而因为较为底层的原因,现在却比较少人关心它,笔者最近在学习一些底层的计算机视觉成像理论,感觉有所裨益,希望能在此进行笔记,作为备忘,如果能对读者有所帮助,则是更好不过了。如有谬误,请联系指正。转载请注明出处。
注意到本文全文采用齐次坐标系的表达方式,具体见[5]。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号: 机器学习杂货铺3号店

相机的针孔模型
为了简单地解释一个相机为什么能够成像,我们通常会引入相机的针孔模型(pinhole model)。如Fig 1.1所示,在针孔模型中,相机呈现的都是倒像,这点其实很好理解,因为光线都是直线传播的,因此物理世界的实体(entity)在相机中的像必然是倒过来的。这里,为了让光只能通过一束(因为只有一束才能确保实体到像的一对一关系,然而实际中不可能做到理想的情况。),我们通常假设这个针孔是无限小的,然而因为无限小的针孔不能透光,为了使得成像有着充足的光线,针孔又必须足够的大,这俩要求显然是个矛盾,因此一般我们需要在针孔处安置透镜,而透镜的引入,包括透镜的厚度,透光度等等不理想的因素,使得成像分析变得复杂起来,但是我们这里还是按照针孔模型的结构去理解,以简化分析。(透镜这里的作用是为了更好的聚集光线。)
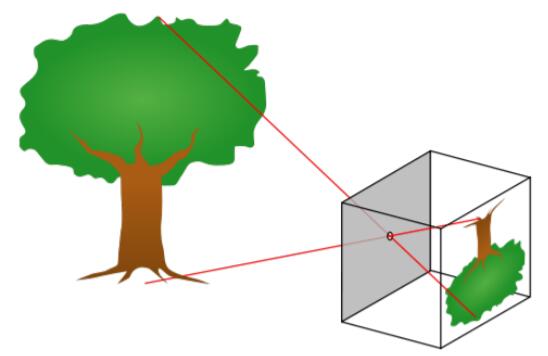
我们需要知道的是,理想的相机模型是不需要透镜的,因为没有透镜的引入,因此成像没有因透镜产生的几何变形和模糊。在这个模型中,我们其实是在描述从实体的3D坐标到成像平面的2D坐标之间的映射关系
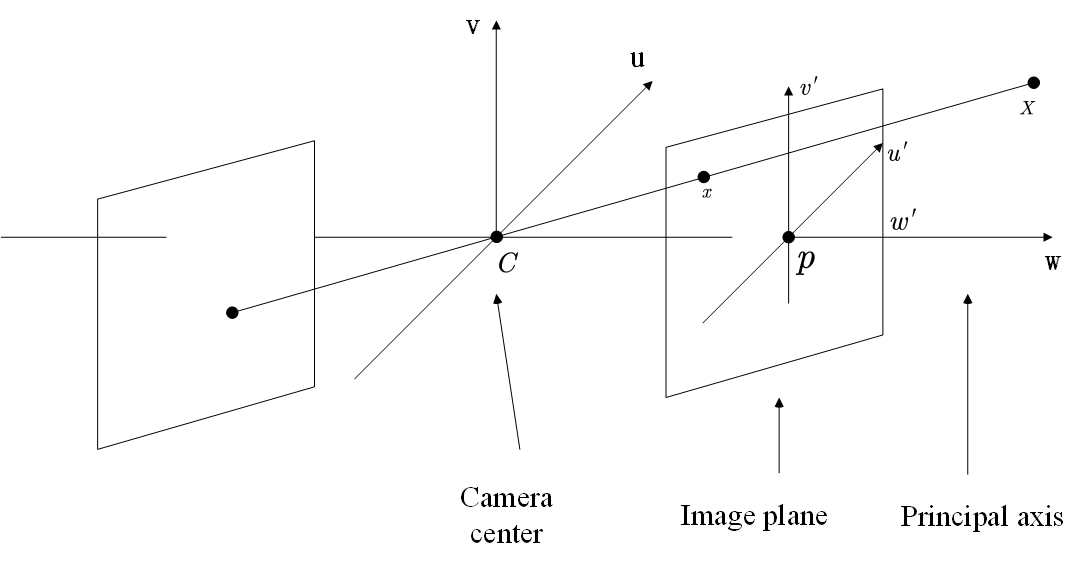
这里,为了方便接下来的讨论,我们将定义和解释以下术语:
- 焦点(camera center, optic center): 所有光线都会聚集的点,比如Fig 1.2中的点C。
- 成像平面(image plane):相机的CCD平面,图像在这个平面上形成,注意后续讨论的image plane一般会是指的呈现正像的那个平面。
- 光轴(principal axis):经过焦点,并且与成像平面垂直的线。
- 光轴面(principal plane): 包含着焦点,并且和成像平面平行的面。
- 焦距(focal length): 通常表示为
,指的是焦点到成像平面的距离。 - 帧(frame): 这里提到的帧和我们通常视频处理里面的帧不太一样,这里提到的帧指的是一种度量,用于衡量一个特定的坐标系系统。
- 世界坐标系(world frame, world coordinate system):一个固定的坐标系,用于表示现实实体的坐标(比如点线面等等)。
- 相机坐标系(camera frame, camera coordinate system):将相机的焦点作为其原点,光轴作为其Z轴的坐标系。
- 图像坐标系(image frame, image coordinate system):描述二维图像的像素位置,通常以图像的左上角或者图像的中心视为坐标原点。
- 外参数(extrinsic parameters): 外参数描述了如何将实体的3D点(以世界坐标系描述)映射到以相机坐标系描述的3D点上,显然,这个是坐标系的平移和旋转过程。
- 内参数(intrinsic parameters):内参数描述了如何将已经是用相机坐标系描述的3D点投射到成像平面上。
- 视网膜平面(image, retina plane):图像在这个平面上成像,注意到,图像平面用相机坐标系度量,其单位是mm,毫米,属于物理单位。
- 图像帧(image frame):这个帧和我们通常理解的帧一致,其用像素(pixel)去描述图像平面,而不是mm了,属于逻辑单位。(比如一个像素对应多少mm的距离是不同的。)
- 光心(principal point): 指的是光轴和成像平面的交点。
这里我们给出一个图取参数上面谈到的一些概念,注意到的是其中的virtual image plane其实是本文中谈到的成像平面。[1]
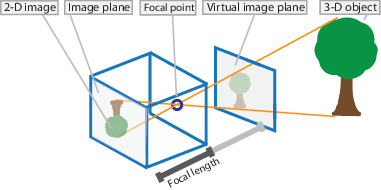
坐标系的改变
为了将一个在世界坐标系中表示的点,以相机坐标系的形式进行表达,我们需要进行坐标系的平移和旋转变化(即是欧几里德变换[4])。比如Fig 2.1所示,我们需要通过平移和旋转将
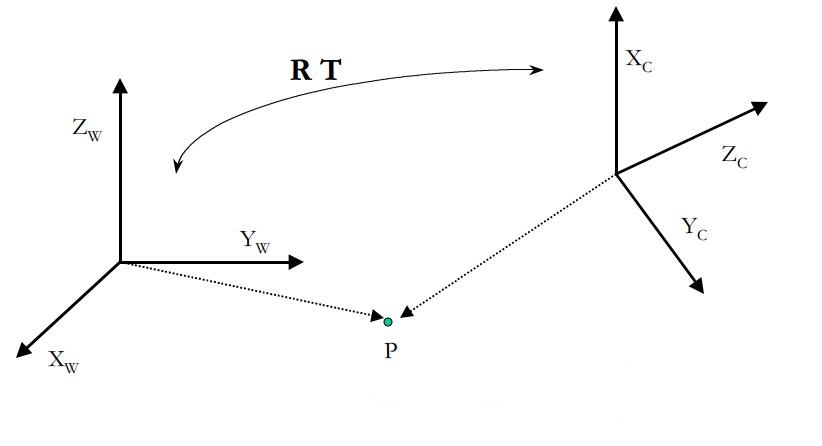
通常来说,这个过程可以简单表示为,平移向量和旋转矩阵的操作,如:
在以上的讨论中,我们把坐标从世界坐标系转换成了相机坐标系,但是我们通常是需要用图像坐标系去表示图片中的某个像素点的,这里涉及到了三维点到二维点的映射问题,因此我们还需要进行 相机坐标系到图像坐标系的转换,即是
我们考虑到在中心投影中,如Fig 2.2中,我们根据相似三角形的规律有,其中以相机坐标系描述的点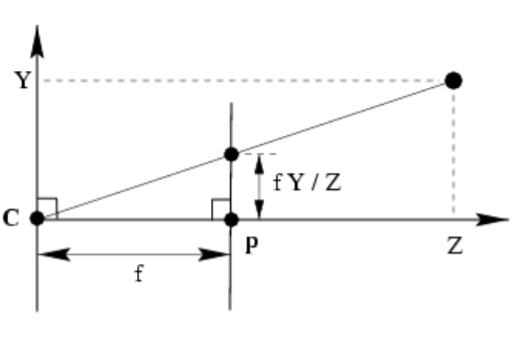
用矩阵形式表达就是:
考虑到公式(2.1)和(2.3),我们能够把一个3D点映射成2D点:
那么总结来说,其实对于坐标系的平移和旋转,我们可以用下面的几副图来表示:
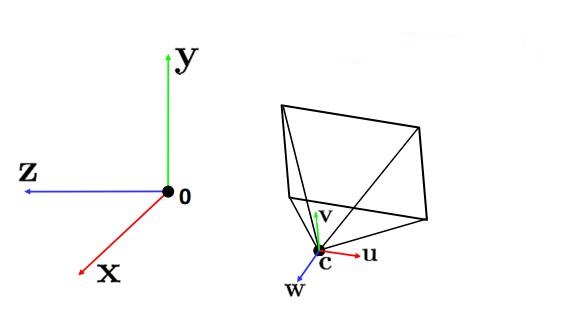
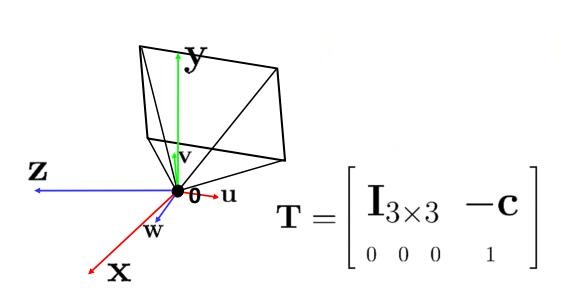
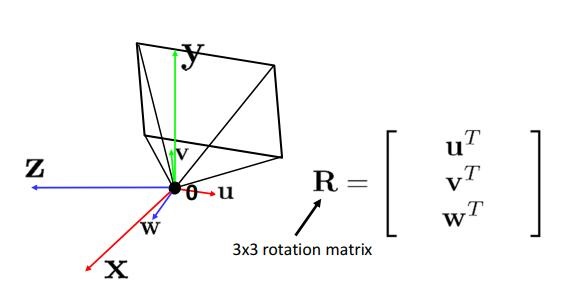
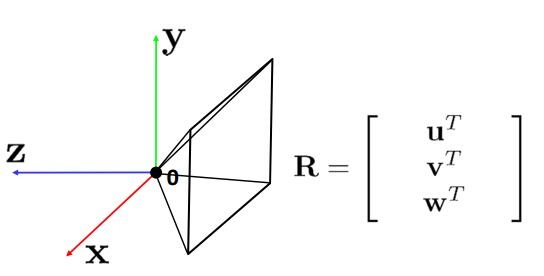
考虑更多因素
注意到通过上面的讨论,我们转换得到的二维像点
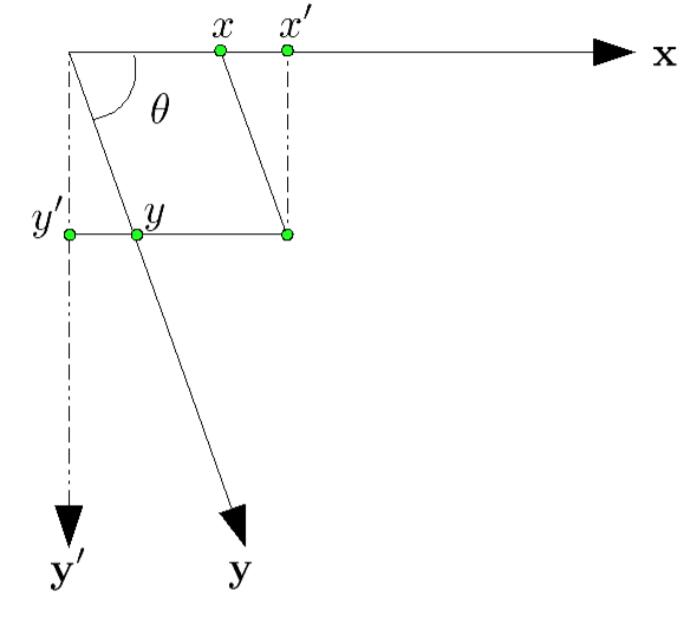
那么经过矫正,其正确的坐标应该是:
其中有
这三个内参数矩阵可以合为一个矩阵
总结
在这篇博文中,我们讨论了相机的针孔模型,其中涉及到了相机的内参数和外参数等,我们将会在以后的文章中发现,这些参数对于相机的呈像是很重要的,因此需要去通过相机标定(camera calibration)去计算这些参数。
Reference
[1]. https://jp.mathworks.com/help/vision/ug/camera-calibration.html
[2]. Forsyth D , JeanPonce, 福赛斯, et al. Computer vision : a modern approach[M]. 电子工业出版社, 2012.
[3]. 电子科技大学自动化学院 杨路 老师 计算机视觉课程课件。
[4]. https://blog.csdn.net/LoseInVain/article/details/104533575
[5]. https://blog.csdn.net/LoseInVain/article/details/102756630