相机一般来说是一种从3D到2D的一种投影工具,其按照数学模型可以分为投影相机,透视相机,弱透视相机和仿射相机等,笔者在本文中尝试对其进行区分和联系。
前言
相机一般来说是一种从3D到2D的一种投影工具,其按照数学模型可以分为投影相机,透视相机,弱透视相机和仿射相机等,笔者在本文中尝试对其进行区分和联系。如有谬误,请联系指正。转载请注明出处。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号: 机器学习杂货铺3号店

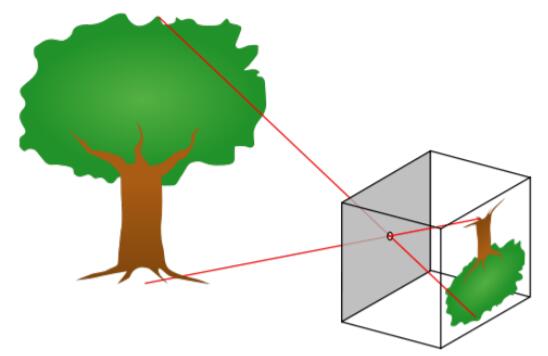
投影相机(projective camera)
相机说到底是一种从3D的现实世界中的点投影到2D平面上点的工具,那么作为这个投影
我们把有这种关系的相机称之为投影相机(projective camera),显然,投影相机是非线性的[7],这里指的非线性是图像显示的尺寸大小和真实尺寸大小不成线性比例,具体见[7]讨论。
透视相机(perspective camera)
投影相机的一种特殊例子也是更为常见的例子是所谓的透视相机(perspective camera),这种相机的投影方式称之为透视投影(perspective projection)或者是中心投影(central projection)。跟一般的,当其变换矩阵
仿射相机(affine camera)
仿射相机也是投影相机的一种特殊情况,其变换矩阵为:
于是,投影后的坐标为:
在仿射相机中,从不同视角观察到的图像的点之间,可以通过一个简单的
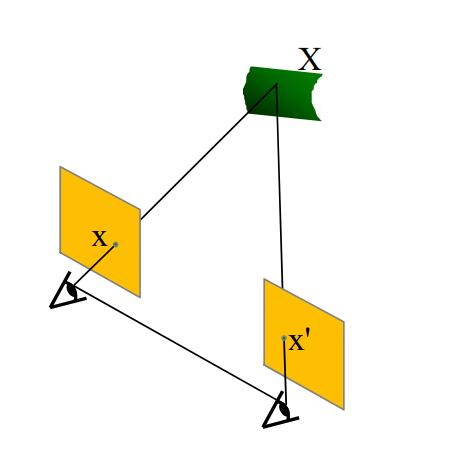
弱透视相机(weak perspective camera)
最常见的,对于相机的假设莫过于是假设其是弱透视相机(weak perspective camera)[10]了。弱透视相机是仿射相机的一种,其最简单的形式是(9),其中的
- 沿着光轴上的,物体的深度的平均差别,也就是
- 视角场(filed of view)(也就是观察某个物体点的夹角,
下面给出证明。
在考虑所有点的深度情况下,我们在
Reference
[1]. http://www.cse.iitd.ernet.in/~suban/vision/affine/node5.html
[2]. http://www.cse.iitd.ernet.in/~suban/vision/affine/node4.html
[3]. http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/UESHIBA1/node5.html
[4]. http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/UESHIBA1/node4.html
[5]. http://www.cse.iitd.ernet.in/~suban/vision/affine/node3.html
[6]. https://blog.csdn.net/LoseInVain/article/details/102756630
[7]. https://blog.csdn.net/LoseInVain/article/details/102869987
[8]. https://blog.csdn.net/LoseInVain/article/details/102756630
[9]. https://blog.csdn.net/LoseInVain/article/details/102632940
[10]. https://blog.csdn.net/LoseInVain/article/details/102698703