支持向量机是常用的，泛化性能佳的，而且可以应用核技巧的机器学习算法，在深度学习流行前是最被广泛使用的机器学习算法之一，就算是深度学习流行的现在，支持向量机也由于其高性能，较低的计算复杂度而被人们广泛应用。这里结合李航博士的《统计学习方法》一书的推导和林轩田老师在《机器学习技法》中的讲解，谈谈自己的认识。

前言

联系方式：

e-mail: FesianXu@gmail.com

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

微信公众号：机器学习杂货铺3号店

SVM的起源

　　支持向量机(Support Vector Machine, SVM)是一种被广泛使用的机器学习算法，自从被Vapnik等人提出来之后便被广泛使用和发展。传统的支持向量机一般是二类分类器，其基本出发点很简单，就是找到一个策略，能够让线性分类器的分类超平面能够最大程度的把两类的样本最好地分割开，这里我们讨论下什么叫做最好地分割开，和实现这个对整个分类器的意义。

最好地分割数据

　　在进行接下来的讨论之前，为了简化我们的讨论从而直面问题所在，我们进行以下假设：

1）我们现在的两类数据是线性可分的，也就是总是存在一个超平面可以将数据完美的分开。 2）我们的数据维度是二维的，也就是特征维只有两个，类标签用+1， -1表示，这样方便我们绘制图像。

　　我在前篇博文《机器学习系列之感知器模型》中已经介绍到了感知器这一简单的线性分类器。感知器很原始，只能对线性可分的数据进行准确分割，而且由于其激活函数选用的是阶跃函数，因此不能通过梯度的方法进行参数更新，而是只能采用错误驱动的策略进行参数更新，这样我们的超平面其实是不确定的，因为其取决于具体随机到的是哪个样本点进行更新，这是一个不稳定的结果。而且，由于采用了这种参数更新策略，感知器的超平面即使是能够将线性数据完美地分割开，也经常会出现超平面非常接近某一个类的样本，而偏离另一个类的样本的这种情况，特别是在真实情况下的数据是叠加了噪声的情况下。　　如下图所示，其中绿线是感知器的运行结果，因为其算法的不稳定性，所以每次的结果都可能不同，选中的这一次我们可以看出来虽然绿线将两类数据完美地分割开了，但是和蓝色样本很接近，如果新来的测试样本叠加一个噪声，这个超平面就很容易将它分类错误，而最佳分类面粉色线则对噪声有着更好地容忍。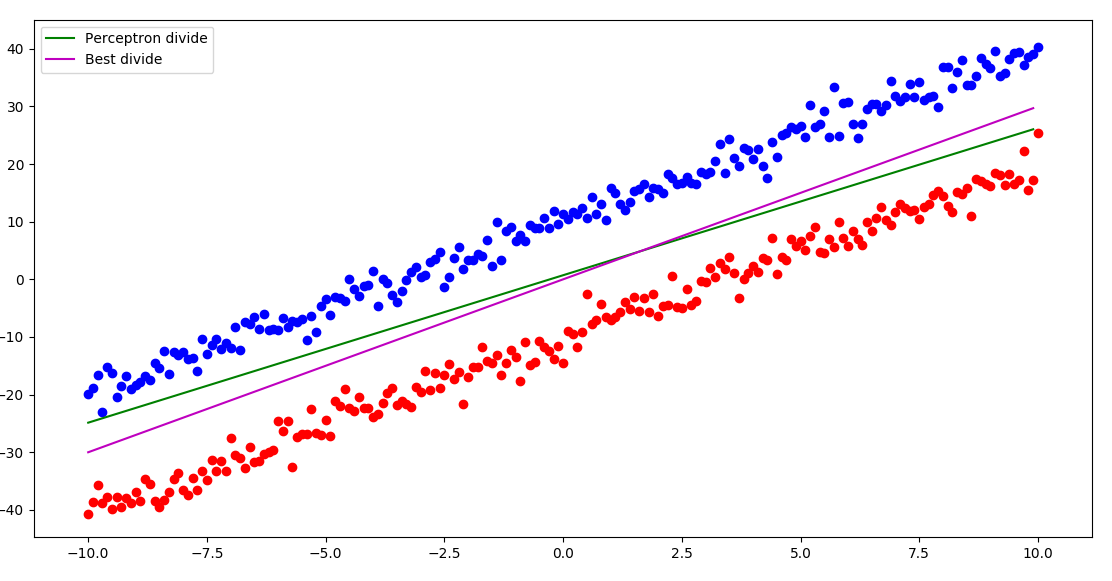

样本噪声

　　刚才我们谈到了样本集上叠加的噪声，噪声广泛存在于真实数据集中，无法避免，因此我们的分类超平面要能够对噪声进行一定的容忍。一般我们假设噪声为高斯噪声，如下图所示：

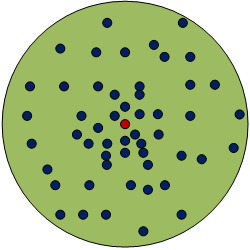
　　其中红点为实际的采样到的样本位置，而蓝点是可能的样本的实际位置，因为噪声的叠加才使得其偏离到了红点位置，其中蓝点的位置满足高斯分布。

最佳分类超平面

　　也就是说我们根据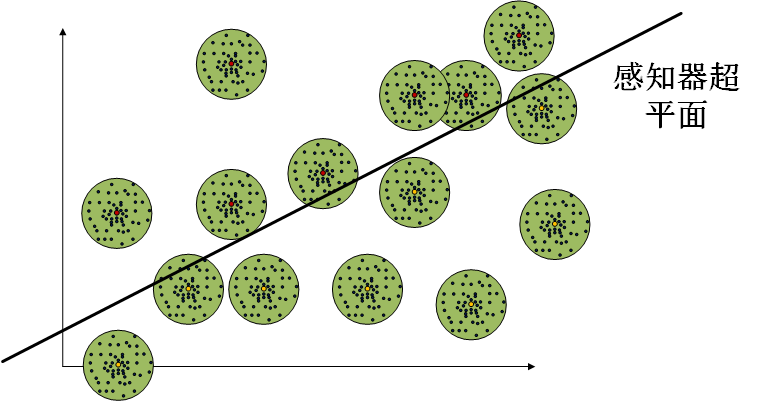点训练出来的感知器的分类器超平面很可能会出现可以完美地划分点，但是却不能正确地划分对新来的测试样本的现象。因为新来的样本很可能位于蓝色的样本点的位置，也就是表现出了严重的过拟合现象，而我们的支持向量机的机制可以很好地减免这种现象，具有更好的泛化能力。我们用几张图来表述下导致这种过拟合的原因：

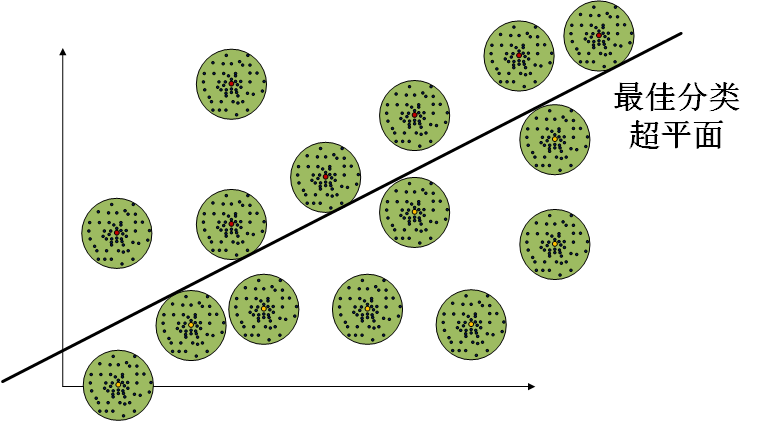
Figure 1, 感知器分类超平面能将线性可分的样本完美分割，但是由于样本叠加了高斯噪声，所以当测试样本的数据出现在超平面“穿过”的“绿圈”之内时，就可能会出现错分的情况，这就是过拟合的一种表现。

Figure 2,假设我们的样本集都是独立同分布采样的，那么其叠加的高斯噪声应该都是相同分布的，因此这个绿圈的大小应该都是相同的，因此最佳的分类超平面应该是可以和距离它最接近的若干个样本的边界相切的。我们把最接近超平面的若干个样本点称为支持向量，支持向量和超平面的距离越远，相当于我们可以容忍的噪声的高斯分布的方差越小，泛化性能越好。注意，这里的高斯分布的方差是我们假设的，不一定是实际数据集叠加的高斯噪声分布的方差，但是假设的越大，总是能带来更好的泛化能力。

SVM提出

　　我们在上面谈到了最佳分类超平面应能够使得支持向量距离超平面的距离最大，这个就是支持向量机的基本机制的最优化的目标，我们需要解决这个问题就必须要先数学形式化我们这个目的，只有这样才能进行最优化和求解。

数学形式化表述

　　我们这里对SVM问题进行数学上的形式化表述，以便于求解，这里主要讨论SVM的原问题，实际上，SVM通常转化为对偶问题进行求解，我们将在下一篇文章里讨论SVM的对偶问题。

函数间隔和几何间隔

　　我们刚才的表述中，我们知道了SVM的关键就是：使得支持向量距离分类超平面的距离之和最小，这里涉及到了“距离”这个概念，因此我们就必须要定义这个“距离”。这个距离可以定义为函数间隔(functional margin)和几何间隔(geometric margin)。我们分别来观察下这两个间隔。

函数间隔

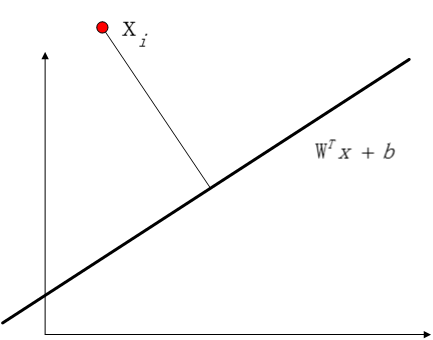
　　我们表征一个样本点到达一个超平面的距离，直接可以表述为: 　　其中为正确的标签，为或，乘上的目的是当分类正确的时候为正，而当分类错误的时候，为负，负数的最大值不超过0，所以也就不存在最大间隔了。整个式子也很好理解，当使得时，该样本点就处于超平面上，当使得大于0时，该样本点处于超平面之外，该值越大离超平面就越远。

几何间隔

　　函数间隔可以在一定程度上表征距离，但是存在一个问题，就是在和同时增大一个相同的倍数时，变成时，因为当时，其零点还是相同的，所以表示的还是相同的超平面。但是我们从函数间隔的定义中可以看出，如果两者都放大倍，那么其函数间隔也被放大了倍，这个就不符合我们的需求了，我们希望的是只要是相同的一个样本点和一个固定的超平面，那么它们之间的距离应该是一定的，这个也是符合我们直观的。因此我们将函数间隔标准化，定义了几何间隔：　　是L2范式，由于这个标准化因子的作用，使得的值不会随着放大因子的变化而变化了。很容易看出：

最大化最小距离

　　定义了几何间隔和函数间隔之后，我们就需要最大化最小距离了，这个听起来挺绕口的，其实意思很简单，就是求得一组和的情况下的最小样本距离，然后在不同的和的情况下最大化这个最小样本距离，最后得出的结果就是能够使得支持向量到超平面的距离最大的超平面了。我们观察下公式可能会更直观一些：

这个就是最小几何间隔距离，我们现在最大化它，有：将两者写在一起，可以表述为：

容易看出其中的其实是和约束条件等价的。我们做一些恒等变换有:

　　这里我们要想一下：的具体取值会不会影响到最优化后的和的取值呢？答案是不会的，因为我们只要令所有支持向量，也就是距离超平面最近的若干个样本点到超平面的距离为单位量，比如为1即可，这个可以通过等比例调整和容易地做到，其他样本也会随着进行相应的缩放。这样对整个超平面的最优化点是没有任何影响的。所以我们现在将设为常数1。现在有：

此时最大化问题转化为最小化问题：

至此，我们得到了SVM的标准原问题表达。注意到这个式子里的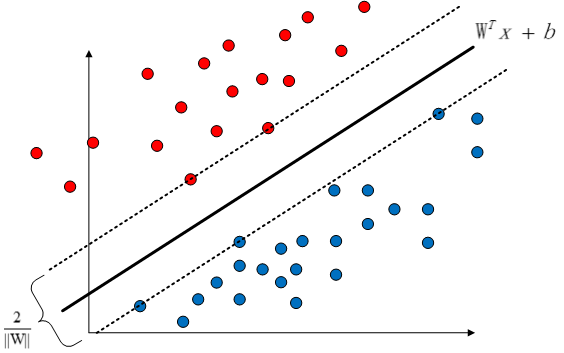，当存在使得时，这个就被称之为支持向量。如下图的虚线上的红色样本和蓝色样本所示，虽然样本有很多个，但是有效的，决定超平面的样本，也就是支持向量一共就只有五个，其到决策面的距离被标准化为了1。

我们接下来将会讨论SVM原问题拉格朗日函数形式以及其对偶问题，以便于更好地解决这个最优化问题。