在SVM的推导中,出现了核心的一个最优化问题,这里我们简单介绍下最优化问题,特别是带有约束的最优化问题,并且引入拉格朗日乘数法和广义拉格朗日乘数法,介绍并且直观解释了KKT条件,用于解决带约束的最优化问题。本人无专业的数学学习背景,只能在直观的角度上解释这个问题,如果有数学专业的朋友,还望不吝赐教。
前言
在SVM的推导中,出现了核心的一个最优化问题,这里我们简单介绍下最优化问题,特别是带有约束的最优化问题,并且引入拉格朗日乘数法和广义拉格朗日乘数法,介绍并且直观解释了KKT条件,用于解决带约束的最优化问题。本人无专业的数学学习背景,只能在直观的角度上解释这个问题,如果有数学专业的朋友,还望不吝赐教。 如有误,请联系指正。转载请注明出处。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号:机器学习杂货铺3号店

最优化问题
我们在高中,包括在高数中都会经常遇到求解一个函数的最小值,最大值之类的问题,这类问题就是属于最优化问题。比如给出下列一个不带有约束的最优化问题:
其中的
因为此时的约束条件是仿射函数(affine function)1,所以可以利用换元法将
拉格朗日乘数法(Lagrange multipliers)
我们先一般化一个二元最优化问题为
将目标函数
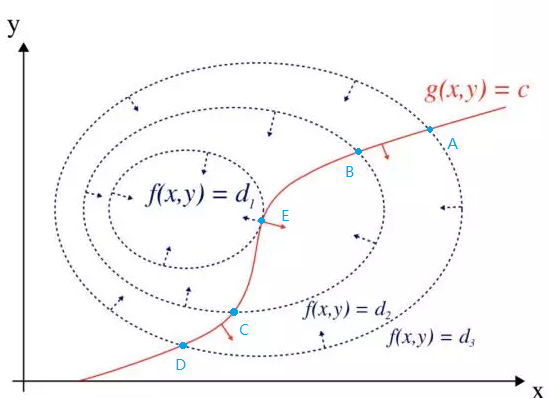
其中的
让我们去掉梯度算子,得出
这个时候
看!我们得出了我们高数中经常见到的等式约束下的拉格朗日乘数函数的表示方法。
多约束的拉格朗日乘数法
以上,我们讨论的都是单约束的拉格朗日乘数法,当存在多个等式约束时(其实不等式约束也是一样的),我们进行一些推广。先一般化一个二元多约束最小化问题:
对于每个目标函数和约束配对,我们有:
将上式相加有:
因为
一个计算例子
让我们举一个单约束的拉格朗日乘数法的计算例子,例子来源于引用3。 给出一个最大化任务:
图像如: 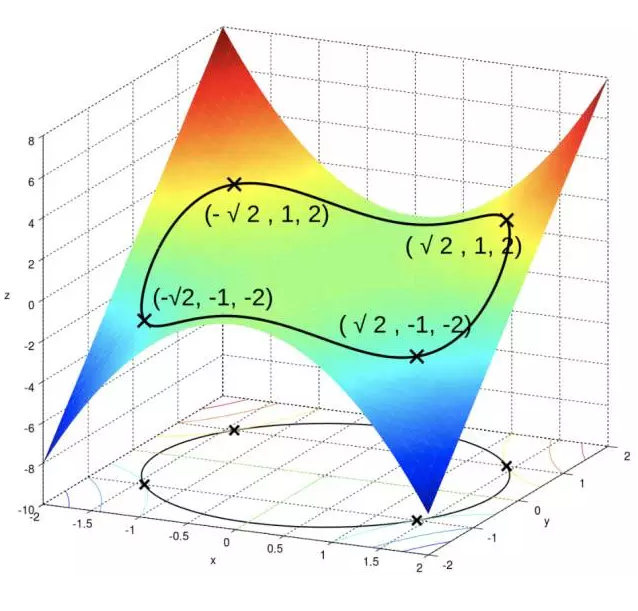 只有一个约束,使用一个乘子
只有一个约束,使用一个乘子
按照条件求解候选点:
有
根据式子
代入
广义拉格朗日乘数法(Generalized Lagrange multipliers)
上面我们的拉格朗日乘数法解决了等式约束的最优化问题,但是在存在不等式约束的最优化问题(包括我们SVM中需要求解的最优化问题)上,普通的拉格朗日乘数法并不能解决,因此学者提出了广义拉格朗日乘数法(Generalized Lagrange multipliers), 用于解决含有不等式约束的最优化问题。这一章,我们谈一谈广义拉格朗日乘数法。 首先,我们先一般化我们的问题,规定一个二元标准的带有不等式约束的最小化问题(当然可以推广到多元的问题),如:
类似于拉格朗日乘数法,参照式子
KKT条件(Karush–Kuhn–Tucker conditions)指出,当满足以下几个条件的时候,其解是问题最优解的候选解(摘自wikipedia)。
- Stationarity
- 对于最小化问题就是:
- 对于最大化问题就是:
- 对于最小化问题就是:
- Primal feasibility
- Dual feasibility
- Complementary slackness
其中的第一个条件和我们的拉格朗日乘数法的含义是相同的,就是梯度共线的意思;而第二个条件就是主要约束条件,自然是需要满足的;有趣的和值得注意的是第三个和第四个条件,接下来我们探讨下这两个条件,以及为什么不等式约束会多出这两个条件。
为了接下来的讨论方便,我们将N设为3,并且去掉等式约束,这样我们的最小化问题的广义拉格朗日函数就变成了:
绘制出来的示意图如下所示: 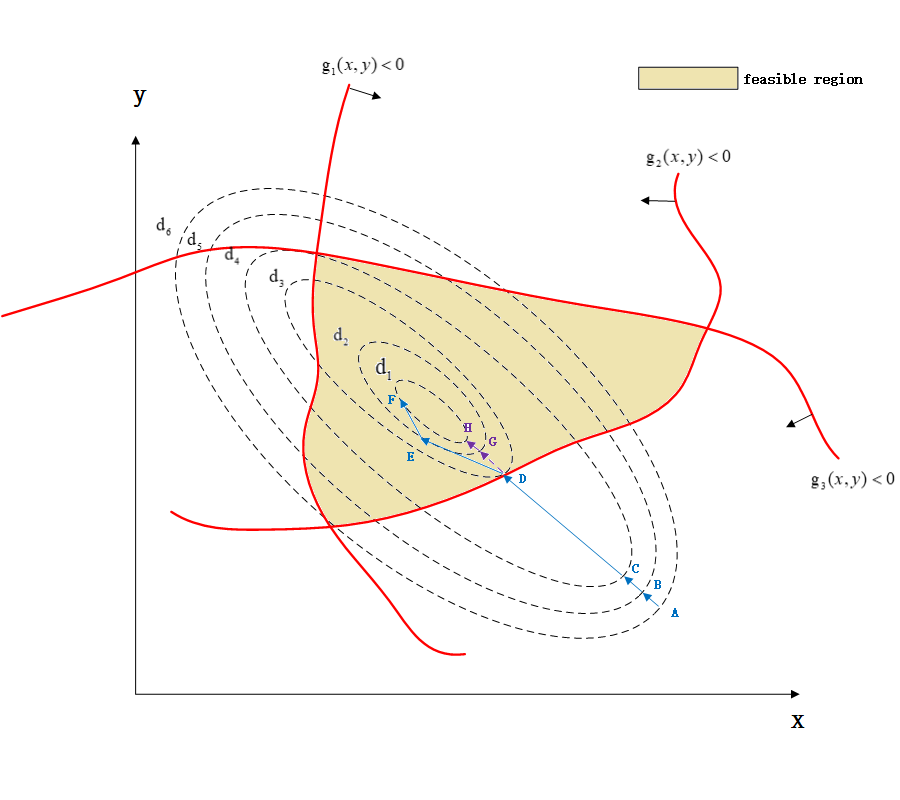 其中
其中
让我们仔细观察式子
我们从上面的示意图入手理解并且记好公式
这就是为什么KKT条件引入了条件3和条件4,就是为了在满足不等式约束的情况下对目标函数进行优化。让我们记住这个条件,因为这个条件中某些
引用
最高次数为1的多项式,形如