在以前的文章中,我们介绍了支持向量机的基本表达式,那是基于硬间隔线性支持向量机的,即是假设数据是完全线性可分的,在数据是近似线性可分的时候,我们不能继续使用硬间隔SVM了,而是需要采用软间隔SVM,在这里我们简单介绍下软间隔线性支持向量机。
前言
在以前的文章中,我们介绍了支持向量机的基本表达式,那是基于硬间隔线性支持向量机的,即是假设数据是完全线性可分的,在数据是近似线性可分的时候,我们不能继续使用硬间隔SVM了,而是需要采用软间隔SVM,在这里我们简单介绍下软间隔线性支持向量机。本人无专业的数学学习背景,只能在直观的角度上解释这个问题,如果有数学专业的朋友,还望不吝赐教。 如有误,请联系指正。转载请注明出处。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号:机器学习杂货铺3号店

软间隔最大化
在文章《SVM的拉格朗日函数表示以及其对偶问题》和《SVM支持向量机的目的和起源》中,我们推导了SVM的基本公式,那时的基本假设之一就是数据是完全线性可分的,即是总是存在一个超平面
但是,在现实生活中的数据往往是或本身就是非线性可分但是近似线性可分的,或是线性可分但是具有噪声的,以上两种情况都会导致在现实应用中,硬间隔线性支持向量机变得不再实用
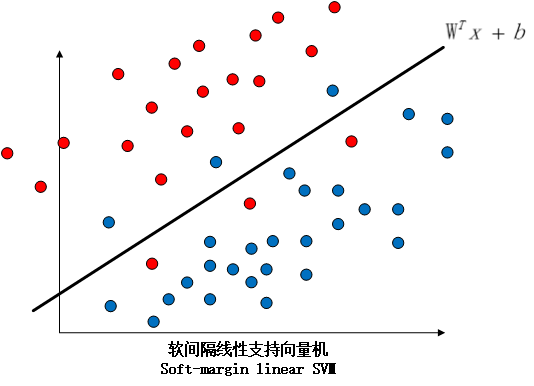
因此,我们引入了软间隔线性支持向量机这个概念,硬间隔和软间隔的区别如下图所示: 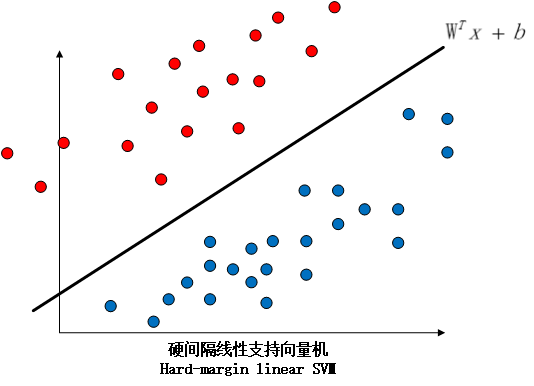
我们的解决方案很简单,就是在软间隔SVM中,我们的分类超平面既要能够尽可能地将数据类别分对,又要使得支持向量到超平面的间隔尽可能地小。具体来说,因为线性不可分意味着某些样本点不能满足函数间隔大于等于1的条件,即是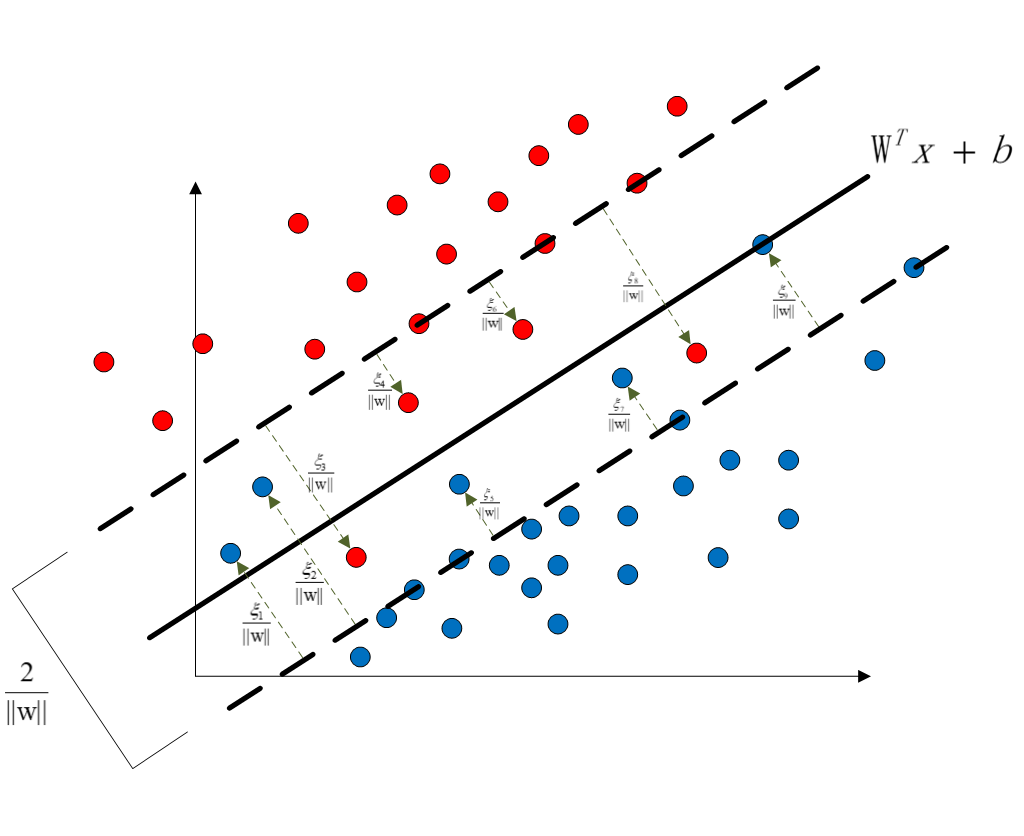 超平面两侧对称的虚线为支持向量,支持向量到超平面的间隔为1。在硬间隔SVM中本应该是在虚线内侧没有任何的样本点的,而在软间隔SVM中,因为不是完全的线性可分,所以虚线内侧存在有样本点,通过向每一个在虚线内侧的样本点添加松弛变量
超平面两侧对称的虚线为支持向量,支持向量到超平面的间隔为1。在硬间隔SVM中本应该是在虚线内侧没有任何的样本点的,而在软间隔SVM中,因为不是完全的线性可分,所以虚线内侧存在有样本点,通过向每一个在虚线内侧的样本点添加松弛变量
软间隔SVM的拉格朗日函数表述和对偶问题
我们采用《SVM的拉格朗日函数表示以及其对偶问题》中介绍过的相似的方法,将
整理得到:
通过将
不难发现软间隔SVM只是在对拉格朗日乘子