笔者在之前的大规模对比学习训练过程(训练CLIP)中,发现在混合精度训练时候,对比学习的交叉熵损失(带温度系数)容易出现的一个小问题,特此笔记下,希望对读者有所帮助。
前言
笔者在之前的大规模对比学习训练过程(训练CLIP)中,发现在混合精度训练时候,对比学习的交叉熵损失(带温度系数)容易出现的一个小问题,特此笔记下,希望对读者有所帮助。如有谬误请联系指出,本文遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明并且联系笔者,谢谢。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号:

在对比学习训练过程中,经常会采用带温度系数的交叉熵损失,如式子(1-1)所示 np.exp(logit/t)为[ 54.59815003 403.42879349 148.4131591 148.4131591 ],对比其原始的打分[0.2 0.3 0.25 0.25],我们从式子(1-1)中已经知道损失函数是正样本打分/样本打分总和的相反数,而当通过指数函数进行放大后,其损失就从原始的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30def cross_entropy(logit, t, ind_pos=0):
print(logit)
print(np.exp(logit/t))
return -np.log(np.exp(logit[ind_pos]/t) / np.exp(logit/t).sum())
orig_score = [0.2,0.3,0.25,0.25]
orig_score = np.array(orig_score)
y0p05 = cross_entropy(orig_score, 0.05)
print(y0p05)
# 输出 loss: 2.626523375036445
# logit: [0.2 0.3 0.25 0.25]
# np.exp(logit/t): [ 54.59815003 403.42879349 148.4131591 148.4131591 ]
y0p5 = cross_entropy(orig_score, 0.5)
print(y0p5)
# 输出 loss: 1.4887933201471417
# logit: [0.2 0.3 0.25 0.25]
# np.exp(logit/t): [1.4918247 1.8221188 1.64872127 1.64872127]
y1p0 = cross_entropy(orig_score, 1.0)
print(y1p0)
# 输出 loss: 1.4369192960265726
# logit: [0.2 0.3 0.25 0.25]
# np.exp(logit/t): [1.22140276 1.34985881 1.28402542 1.28402542]
y2p0 = cross_entropy(orig_score, 2.0)
print(y2p0)
# 输出 loss: 1.4114506070510497
# logit: [0.2 0.3 0.25 0.25]
# np.exp(logit/t): [1.10517092 1.16183424 1.13314845 1.13314845]
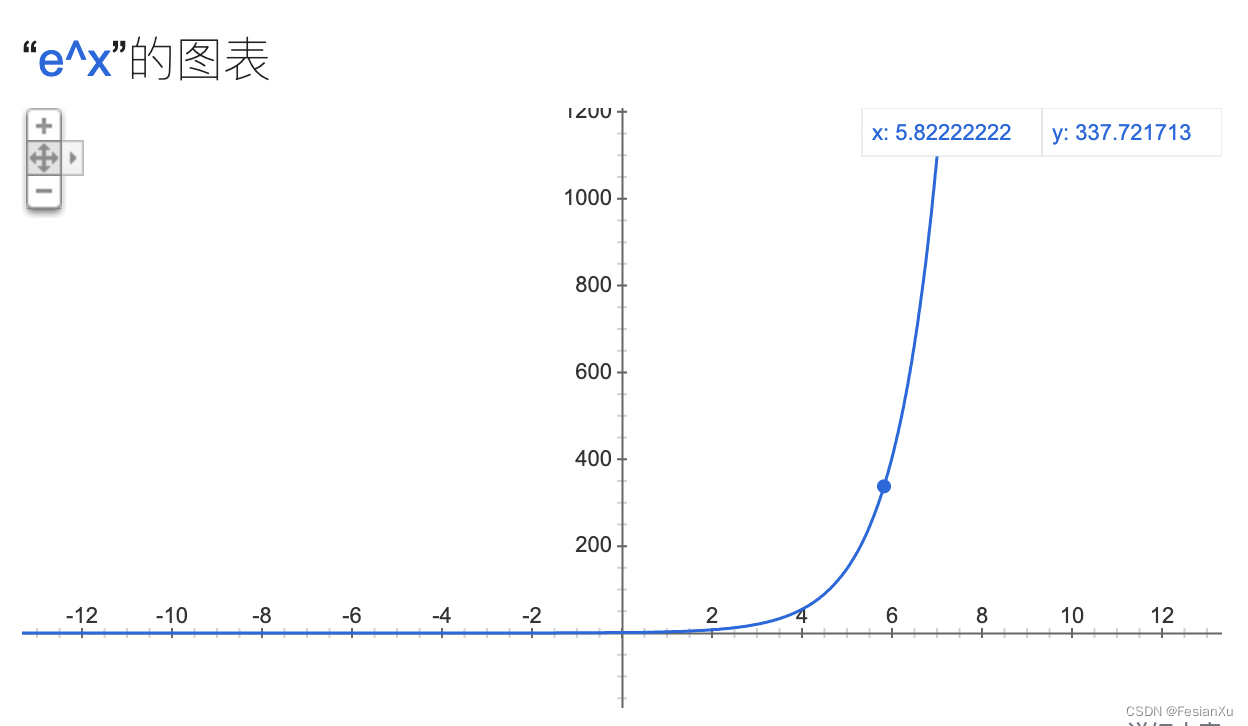
然而,当训练到一定程度时候,模型的打分已经比较置信了,假设为1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16# logit: [0.7 0.1 0.05 0.15]
# np.exp(logit/t): [1.20260428e+06 7.38905610e+00 2.71828183e+00 2.00855369e+01]
# 输出 loss: 2.5105927394272577e-05
====
# logit: [0.7 0.1 0.05 0.15]
# np.exp(logit/t): [4.05519997 1.22140276 1.10517092 1.34985881]
# 输出 loss: 0.6453200240879728
====
# logit: [0.7 0.1 0.05 0.15]
# np.exp(logit/t): [2.01375271 1.10517092 1.0512711 1.16183424]
# 输出 loss: 0.9737318345317211
====
# logit: [0.7 0.1 0.05 0.15]
# np.exp(logit/t): [1.41906755 1.0512711 1.02531512 1.07788415]
# 输出 loss: 1.1702870665310683
====
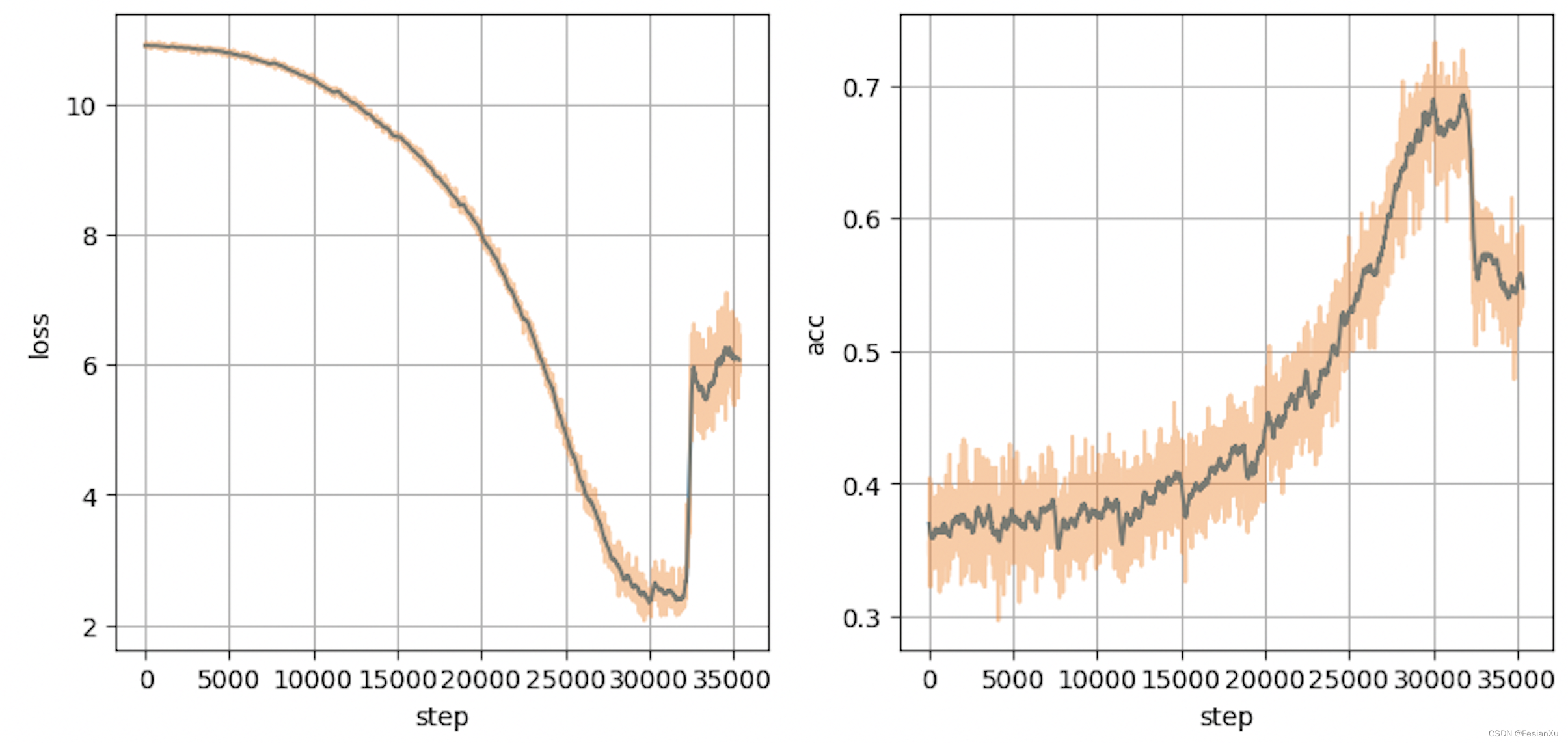
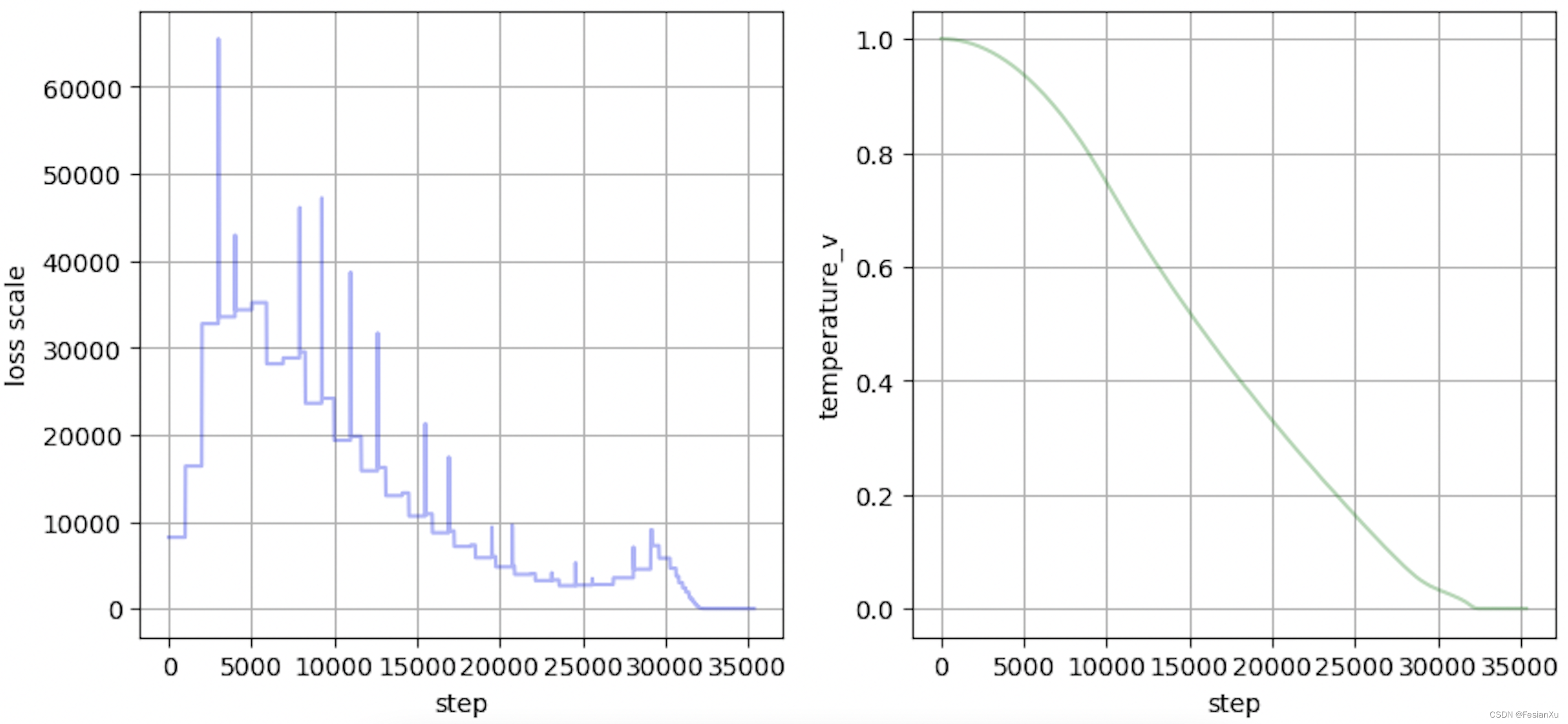
然而手动在不同阶段调节温度系数很麻烦,而且可能并不是最优的,因此就有人尝试将温度系数设置为可学习的(learnable temperature),通过梯度更新温度系数。这一点在全精度训练下并没有太大问题,但是为了加大训练的batch size,通常会在半精度场景中进行训练(auto mixed precision,amp),此时容易出现下溢出的问题,损失函数如Fig 2.所示,训练过程会突然崩溃,此来龙去脉且听笔者道来。
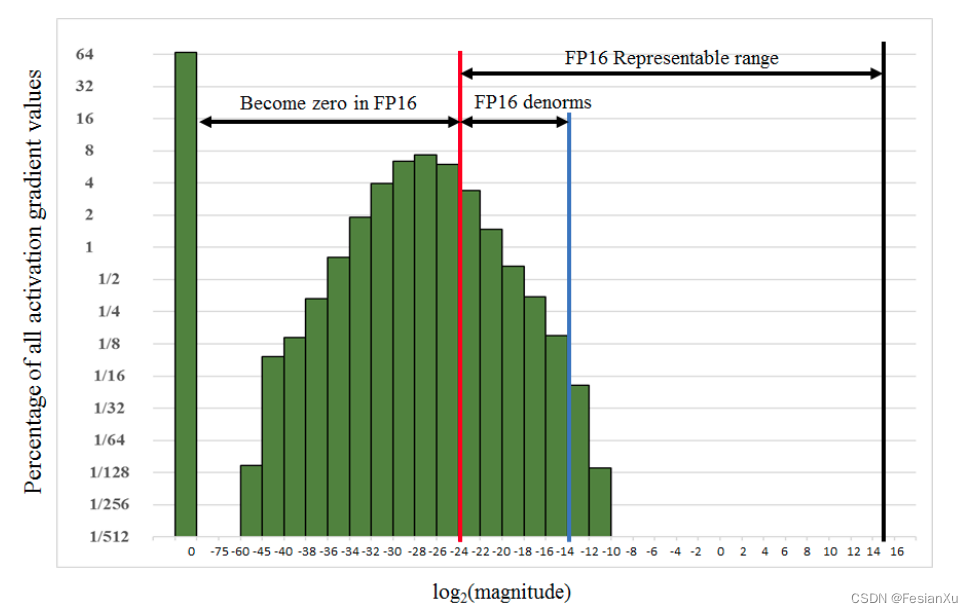
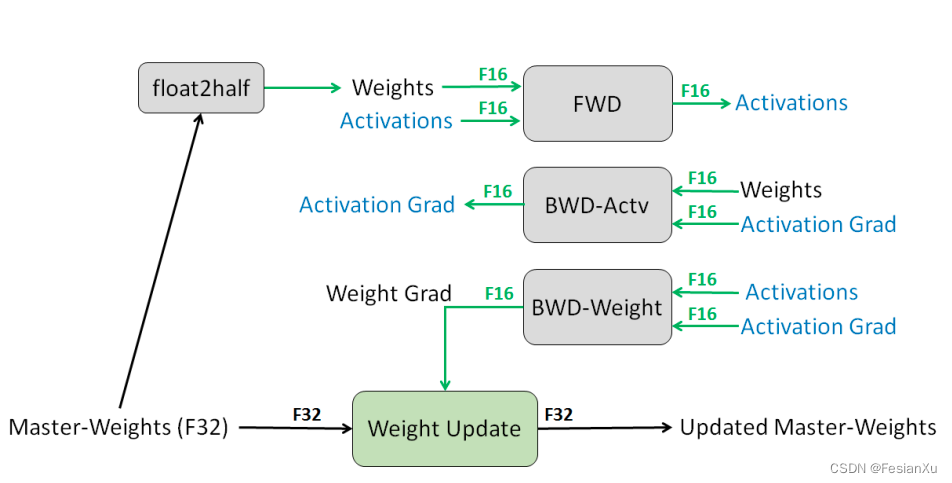
我们以paddle的半精度训练为例子,如文档[3]所示,半精度即是FP16。如Fig 3.所示,此时实际情况中模型训练中的某些变量, 比如grad (特别是 activation 的 grad), 可能会因小于 FP16的精度低而变成0 (红色线条以左); 另一方面在FP16 的表示范围的中有很大的一部分(从蓝色线最大值往右) 却没有被利用到,导致整个分布(绿色方块)只有一小部分(红线-蓝线之间)落在FP16的表示范围内。此时对梯度的数值进行整体的一个放大(或者缩小),能够更充分的利用FP16 的表示范围。AMP 会在反向开始前对 loss 进行放大,并在执行任何梯度相关操作(e.g. gradient-clip, update) 之前对 gredient 进行缩放恢复原来的大小。
通常来说,框架会提供动态损失放缩(Dynamic loss scaling)的机制,此时框架会检测scale大小是否合适,当scaling up 不足时,仍会有部分较小变量会被表示成 0而损失精度;当scaling up 过度时,变量超过FP16表示范围出现 nan or inf, 同样造成精度损失。此时动态损失放缩会采用自动检测梯度值的方法:
当连续
incr_every_n_steps(int)个batch 中所有的gradient 都在FP16 的表示范围, 将scaling factor 增大incr_ratio(float)倍;当有连续decr_every_n_nan_or_inf(int)个batch 中gradient 里出现 nan / inf时, scaling factor 缩小decr_ratio(float)倍.
如Fig 4.所示,在 Dynamic loss scaling 中,框架在每一个 iteration 都会依据当前 gradients 是否出现 nan or inf 还有用户设置的 Dynamic loss scaling 参数来动态调整 loss scaling factor 的大小,将gradient 尽量保持在 FP16 的表示范围之内。
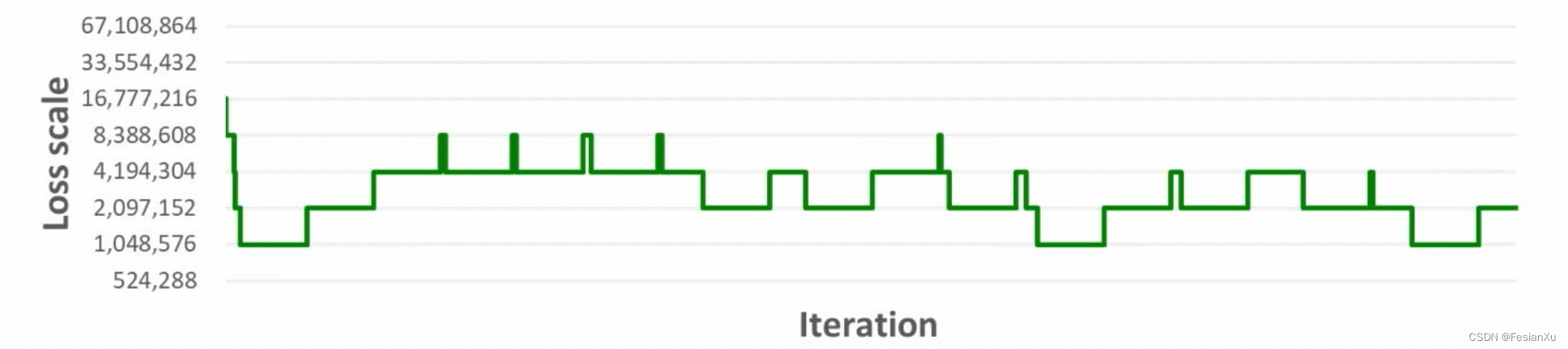
然而,如果在半精度场景中把温度系数设置为可学习的,通过之前的讨论我们知道温度系数控制了整个学习任务的难易程度,同时其也可以控制损失大小,也就意味着在训练到某个阶段,模型可能会倾向于连续降低温度系数以进一步降低损失(此时继续优化模型参数本身需要更多的iteration,但是『优化』温度系数会获得短期更快的损失下降)。此时温度系数会持续下降,如Fig 5.右图所示,而温度系数一直下降意味着loss scale持续下降(否则就超过了FP16的表示范围),知道loss scale降到了0都无法挽救为止,此时训练将会出现nan或者inf,导致训练过程崩塌。
怎么缓解这个问题呢?笔者实践中是将温度系数固定在0.05开始模型从头的训练,等模型训练到差不到的时候才开放温度系数的可学习性。
补充
在知乎有个朋友问了个有意思的问题,感觉值得写个补充回答,因而在博客这里回答下,知乎链接:https://zhuanlan.zhihu.com/p/526175260,问题为:
serendipity: 根据文章所述,训练崩溃的原因是:网络在优化的时候倾向于缩小温度系数,然而这会导致
太大,发生梯度爆炸,即使 loss_scale变成0也拉不回fp16的表示范围。如果是这样的话,即使用fp32也会遇到训练崩溃的问题吧,缩小温度系数导致梯度爆炸。
首先注意到,loss scale是在混合精度训练过程中才存在的概念,这个用于将值的表示范围平衡到fp16的有效范围内,而在fp32中是没有这个概念的。因此这里的逻辑链条其实应该是,由于在fp16的情况下,温度系数倾向于缩小(但不会一直缩小,按我的经验应该是会下降到0.05左右的量级),此时loss scale一直下降。我们从IEEE 754中可知道FP16的表示范围在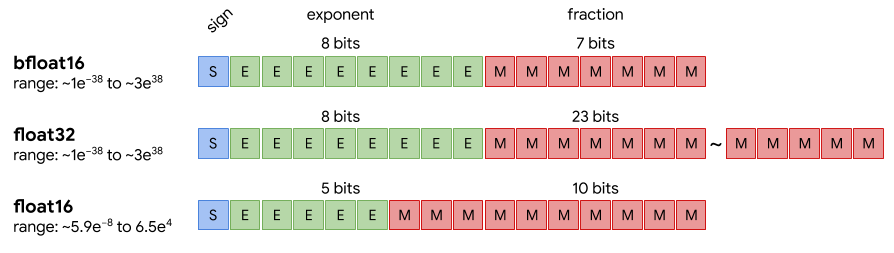
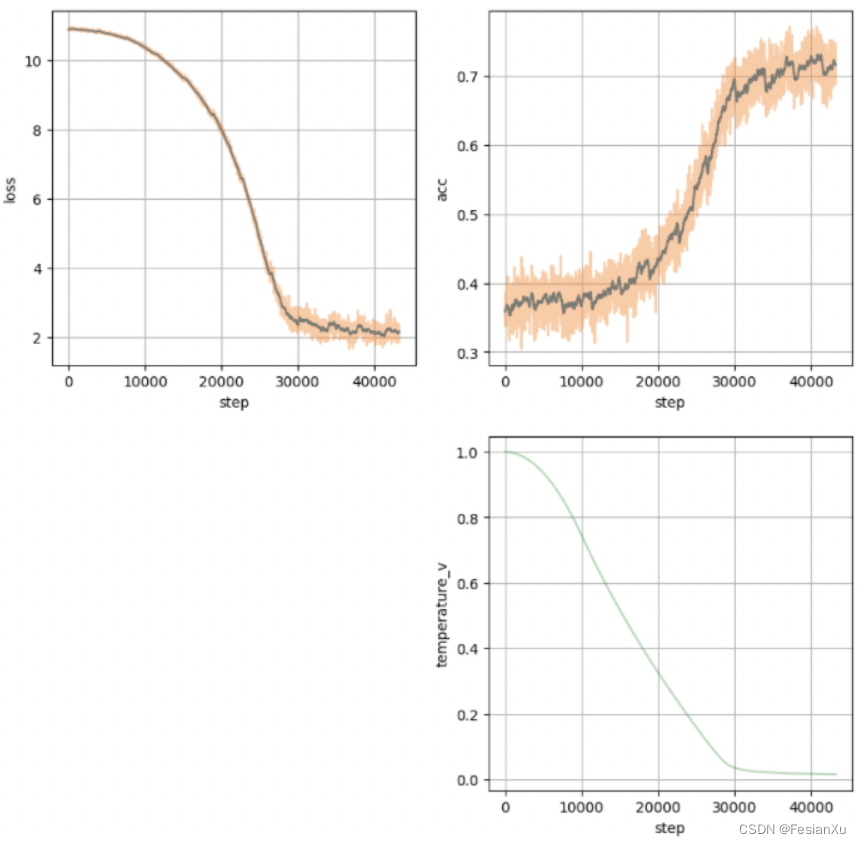
但是问题的关键并不在此,问题在于如Fig A2所示,在大于30000步后的某个瞬间,温度系数loss scale也随着『骤降』到0了。如何理解这个温度系数的骤降呢?笔者个人是这样理解的,注意到混合精度训练机制下,是对梯度进行检测是否在有效FP16范围内,从而对loss进行放缩的,而其中间的计算值(如激活值)是不会被检测的。同时,如Fig A3所示,在混合精度训练过程中,中间计算结果(如激活值),反向的梯度等是用FP16表示的,也就是说一旦温度系数太小,导致loss scale是通过检测梯度变化才会改变的,此时loss scale对其是无能为力的。这里出现的inf将会导致梯度出现inf,使得loss scale缩小decr_ratio(float)倍,然而即便如此,在训练的过程中仍然会不断持续出现inf(主因是FP16的表示范围太小了,很容易就会超出65000的上限),因此loss scale一直缩小decr_ratio(float)倍,极其快速地达到了0(下溢出了)。注意到一旦loss scale变成0,就再也无法脱离0这个命运了,因为无论0乘上何数都为0。不过笔者暂时对为何此处温度系数也会突然骤降到0还不是很理解,上面的解释暂时没法解释这个现象。
正常的FP32的训练过程如Fig A4所示,FP32的表示范围比FP16大太多了(上限高了30多个数量级),其上溢出的风险远远小于FP16,因此也不存在loss scale这种妥协机制。在FP32下训练,其温度系数会逐渐收敛到一个值(比如是0.05左右),而不会一直下降到0,同样此时loss和metric都不会崩溃,能够正常训练。 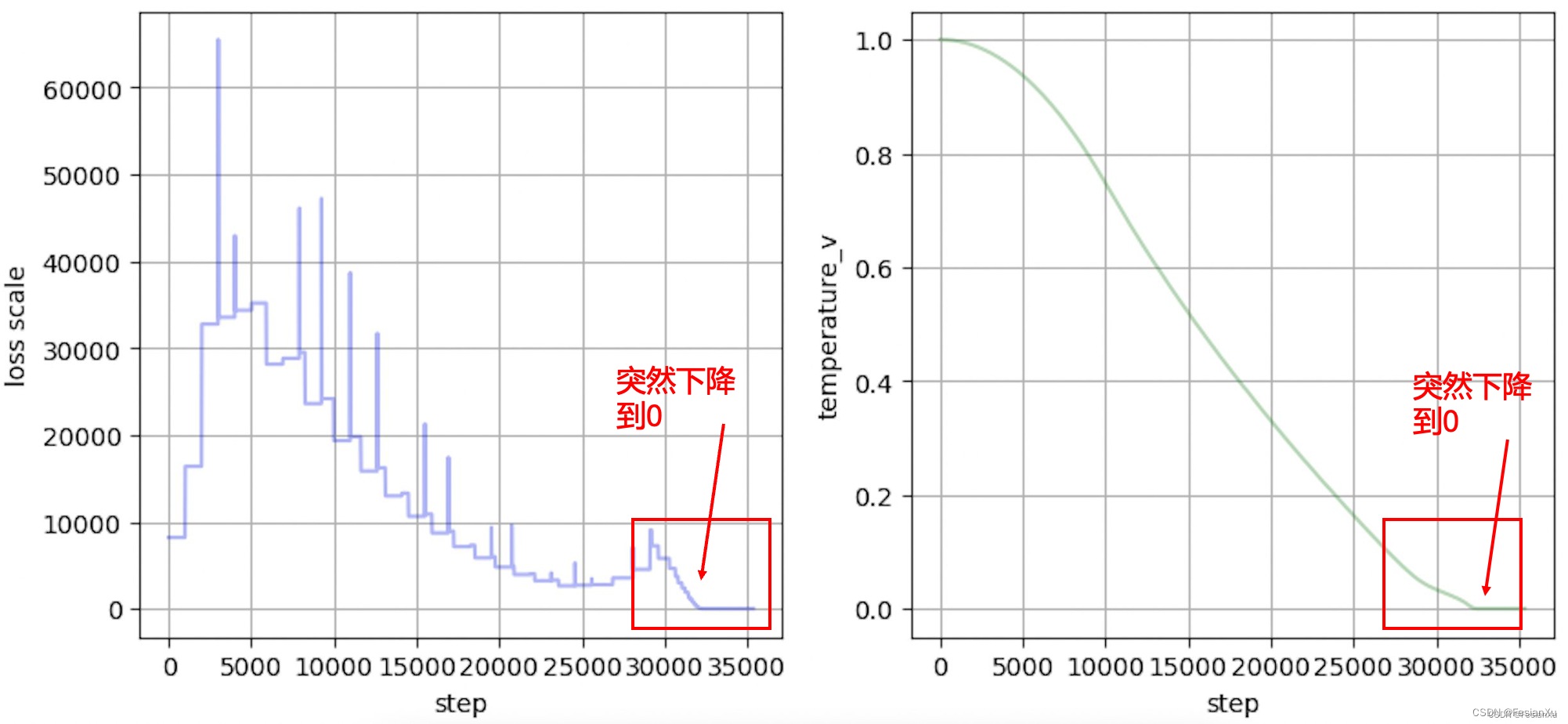
Reference
[1]. https://blog.csdn.net/LoseInVain/article/details/119515146, 《MoCo 动量对比学习——一种维护超大负样本训练的框架》
[2]. https://blog.csdn.net/LoseInVain/article/details/119516894, 《CLIP-对比图文多模态预训练的读后感》
[3]. https://fleet-x.readthedocs.io/en/stable/paddle_fleet_rst/fleet_collective_training_speedup_with_amp_cn.html, 《自动混合精度练加速分布式训练》