最近工作里面遇到了LLM复读的问题,去翻了下论文,看到有一篇尝试通过引入负样本解决复读问题的工作,有所启发,在此简单介绍下,希望对大家有所帮助
前言
最近工作里面遇到了LLM复读的问题,去翻了下论文,看到有一篇尝试通过引入负样本解决复读问题的工作,有所启发,在此简单介绍下,希望对大家有所帮助。如有谬误请见谅并联系指出,本文遵守CC 4.0 BY-SA版权协议,转载请联系作者并注明出处,谢谢。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
github page: https://fesianxu.github.io/
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号:机器学习杂货铺3号店 
LLM的复读问题,一般有几种级别的复读,如下所示
- 字粒度的复读:
User: 你喜欢北京么?
AI: 北京是中国的首都,有很多名胜古迹,如长城,故宫,天坛等,我十分喜欢欢欢欢欢欢欢欢欢欢欢欢….
- 词粒度的复读:
User: 你喜欢北京么?
AI: 北京是中国的首都,有很多名胜古迹,如长城,故宫,天坛等,我十分喜欢喜欢喜欢喜欢….
- 句子粒度的复读:
User: 你喜欢北京么?
AI: 北京是中国的首都,有很多名胜古迹,如长城,故宫,天坛等,我十分热爱北京,我十分热爱北京,我十分热爱北京,…..
贪婪搜索解码(greedy search)由于其解码结果是固定的(deterministic),并且解码速度快等优点,是在实际应用中经常使用的解码方法。在清华大学的一篇论文 [1]中,介绍了一种在贪婪搜索解码的前提下对复读问题的解决方案。如Fig 1 (b)所示,在Wikitext-103 dev数据集上,作者统计了模型生成结果和人类结果在不同粒度(word、 phrase、sentence)下的连续复读占比情况。不难发现人类编写的结果的连续复读占比随着粒度的增大,会快速减少,而模型生成的结果则在句子粒度上的复读中达到了惊人的最大值(~35%)。这说明在贪婪解码中,句子粒度的复读是最常见的复读模式,因此作者对这种模式的形成原因进行了研究。
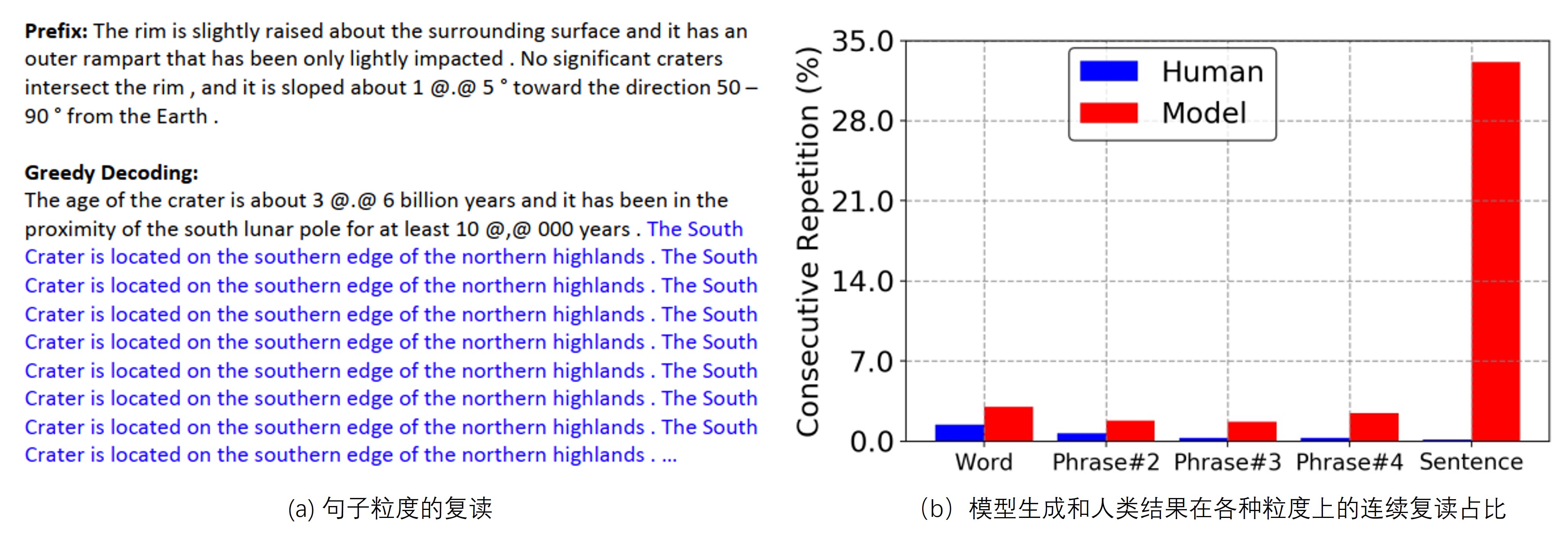
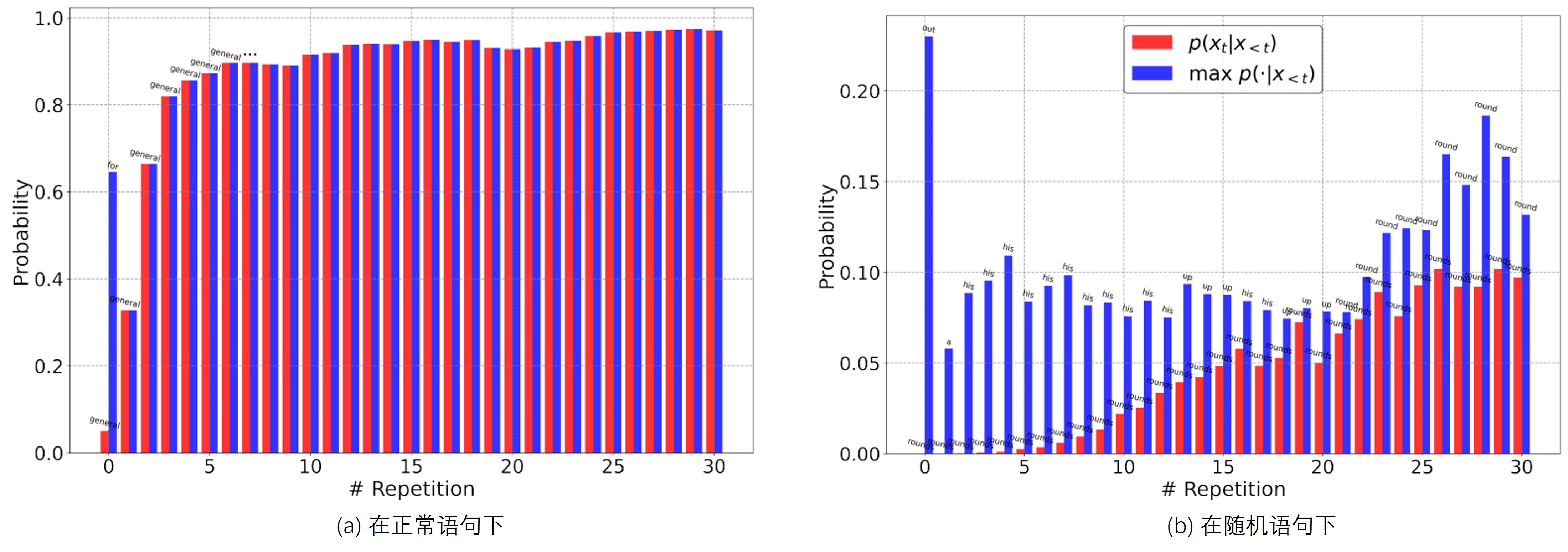
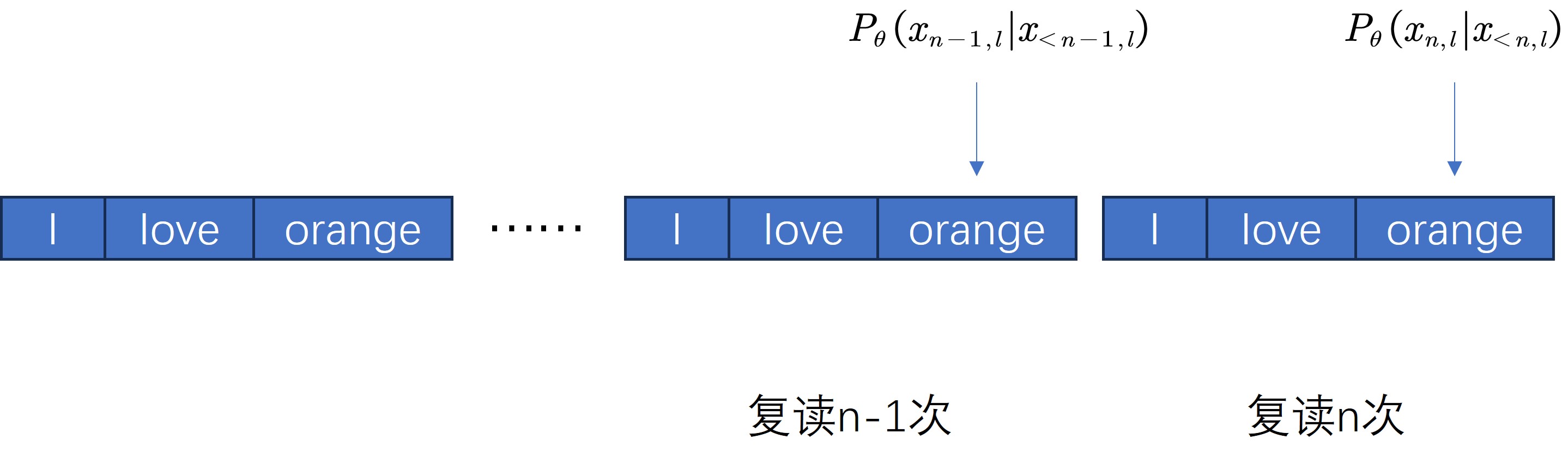
作者研究这个现象的基本方法,可以简单理解为手动重复一个句子,然后研究每个token的生成概率的变化,举个例子就是
用户:和马有关的成语有哪些?
模型:和马有关的成语非常丰富,以下是一些常见的例子: 马到成功:形容事情顺利,刚开始就取得成功。 指鹿为马:指着鹿,说是马。比喻故意颠倒黑白,混淆是非。 马到功成:形容事情顺利,刚开始就取得成功。
此处的第1个成语出现了“马到”,而第3个成语也出现了“马到”,此时如果模型没有训练好,由我们之前得出的自增强结论,将会很容易出现复读现象。这种类型的case在一些排比手法的问答中经常出现,或者是输出有些其他特定的模式的问答中也可能出现。
作者在论文中,同时还对非自然句子进行了观察,如Fig 2 (b)所示,“fría backed rounds Manganiello Benzedrine Magruder Crego Stansel Zemin compressus ”这个句子是随机从词表中挑选而来的,其
当然,以上都是基于采样的一句话进行观察得到的结论,为了让结论更具有普遍性,作者在公开数据集上进行了观察,采用的数据有以下三种:
: 从词表中随机采样得到的句子集合,数量为1000个句子。 : 从Wikitext-103 dev数据集中随机采样得到的1000个句子。 : 从BookCorpus数据集中随机采样得到的1000个句子。
为了更好的定量分析模型在复读下的情况,作者定义了三种不同的指标,首先为了方便理解,需要约定一些符号。假定给定一个数据集
- 平均令牌概率(Average Token Probability): 如公式(1)所示,用以表征在
次复读情况下生成的句子,其句子的所有令牌的令牌概率和,TP越高表示复读产生该句子的概率越高。
令牌概率增加率(Rate of Increased Token Probability): 用于表示在复读n次的情况下,
胜出率(Winner Rate):如果
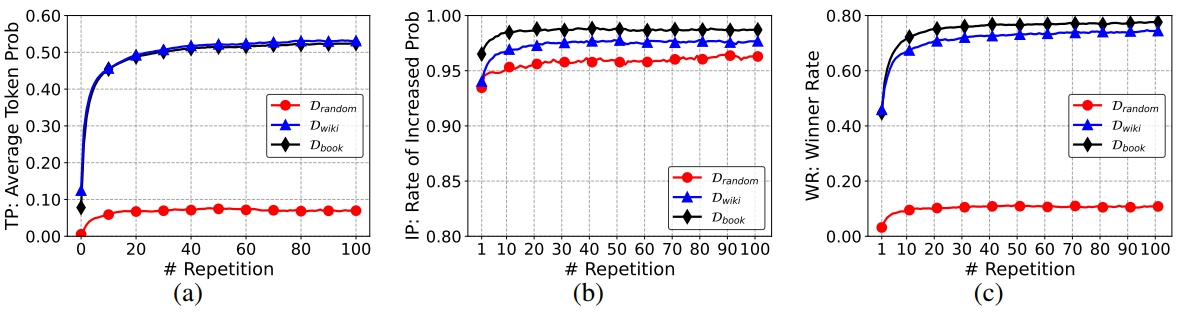
如图Fig 3.所示,这三张图就是在以上三个数据集上统计TP、IP和WR指标的变化,从中我们能得到几个结论:
- 为什么会出现句子粒度的复读? 从Fig 3. (b)可知,
- 为什么模型一旦开始复读,就难以自愈了呢?从Fig 3.中可知,TP、IP和WR都是随着复读次数的增加而单调递增,这意味着句子粒度的复读具有自增强效应,一旦出现复读现象的苗头,就只会越演越烈,难以回头。
- 什么类型的句子容易出现复读呢?作者对比了
从结论来看,模型生成结果有从历史前文中找“捷径”的倾向,由于采用了贪婪搜索解码,导致模型生成结果容易出现复读,而复读具有自增强效应,因此一旦落入复读“陷阱”就难以脱身。既然知道了出现复读的原因,那么怎么去解决呢?
作者提出了一种称呼为DITTO(Pseudo repetition penalization,伪复读惩罚)的方法,其主要思想是手动构建具有复读模式的样本(负样本),混合正常样本(正样本)给模型进行学习,辅以惩罚损失指导模型避免出现复读。 惩罚损失函数如公式(4)所示,首先需要构建伪复读样本,可以考虑从训练集中抽取部分锚点样本,然后对锚点样本复读N次,产生如repetition-4和repetition-sen,由于基准测试集有人工标注因此可以统计人工的复读程度,和这个值接近可以认为效果越好。 我们看到虽然DITTO复读指标上的效果不如UL-token+seq,但是后者牺牲了部分的通用性能。DITTO是以MLE为基线试验的,可以看出确实比起MLE有着很大的提升,因此可以确定DITTO策略的有效性。Fig 5. (b)则是在非贪婪搜索解码中的效果对比,可以发现是DITTO效果最好,但是其实提升就没有第一个试验来得大了,这是因为解码过程采用了采样策略后,复读问题本就会得到极大缓解。
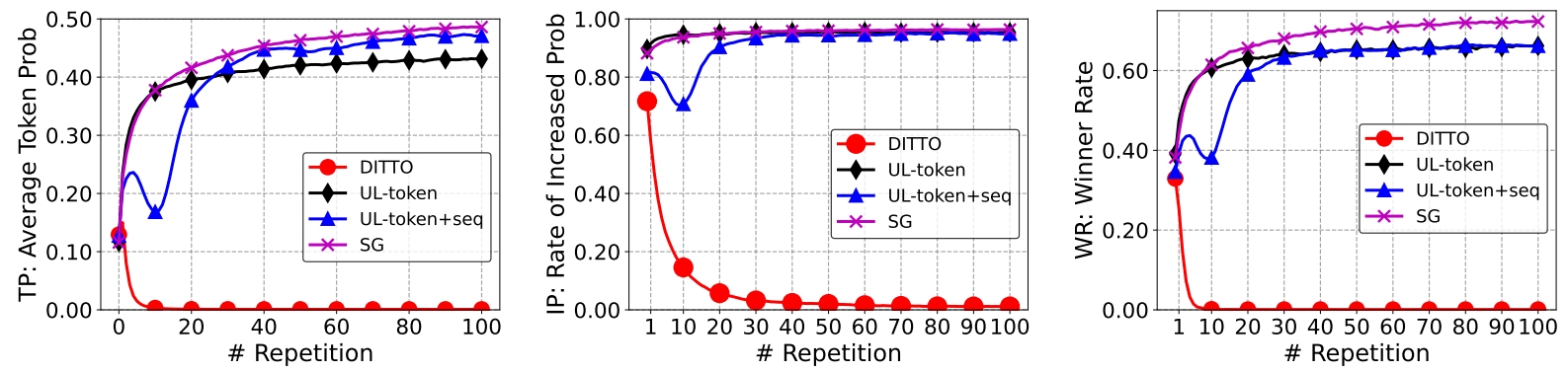
我们再看到采用了DITTO后,TP、IP、WR等指标的变化,如Fig 6所示,我们能发现红线确实符合预期的接近0,这说明引入惩罚之后,复读问题的自增强效应得到了打压。
Reference
[1]. Xu, Jin, Xiaojiang Liu, Jianhao Yan, Deng Cai, Huayang Li, and Jian Li. "Learning to break the loop: Analyzing and mitigating repetitions for neural text generation." Advances in Neural Information Processing Systems 35 (2022): 3082-3095.