搜索系统中的Learning To Rank模型：GBRank

Posted on | In |
Words count in article: 2.7k 字 | Reading time ≈ 9 分钟

Learning To Rank(LTR)模型是对搜索/计算广告/推荐系统中的排序问题进行模型建模的方法，在当前的搜索系统中有着至关重要的作用...

FesianXu 20220326 at Baidu Search Team

前言

Learning To Rank(LTR)模型是对搜索/计算广告/推荐系统中的排序问题进行模型建模的方法，在当前的搜索系统中有着至关重要的作用，本文简单介绍LTR模型中常用的GBRank模型，包括一些基本知识和笔者的理解。如有谬误请联系指出，本文遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明并且联系笔者，谢谢。

联系方式：

e-mail: FesianXu@gmail.com

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

微信公众号

搜索系统中的排序问题

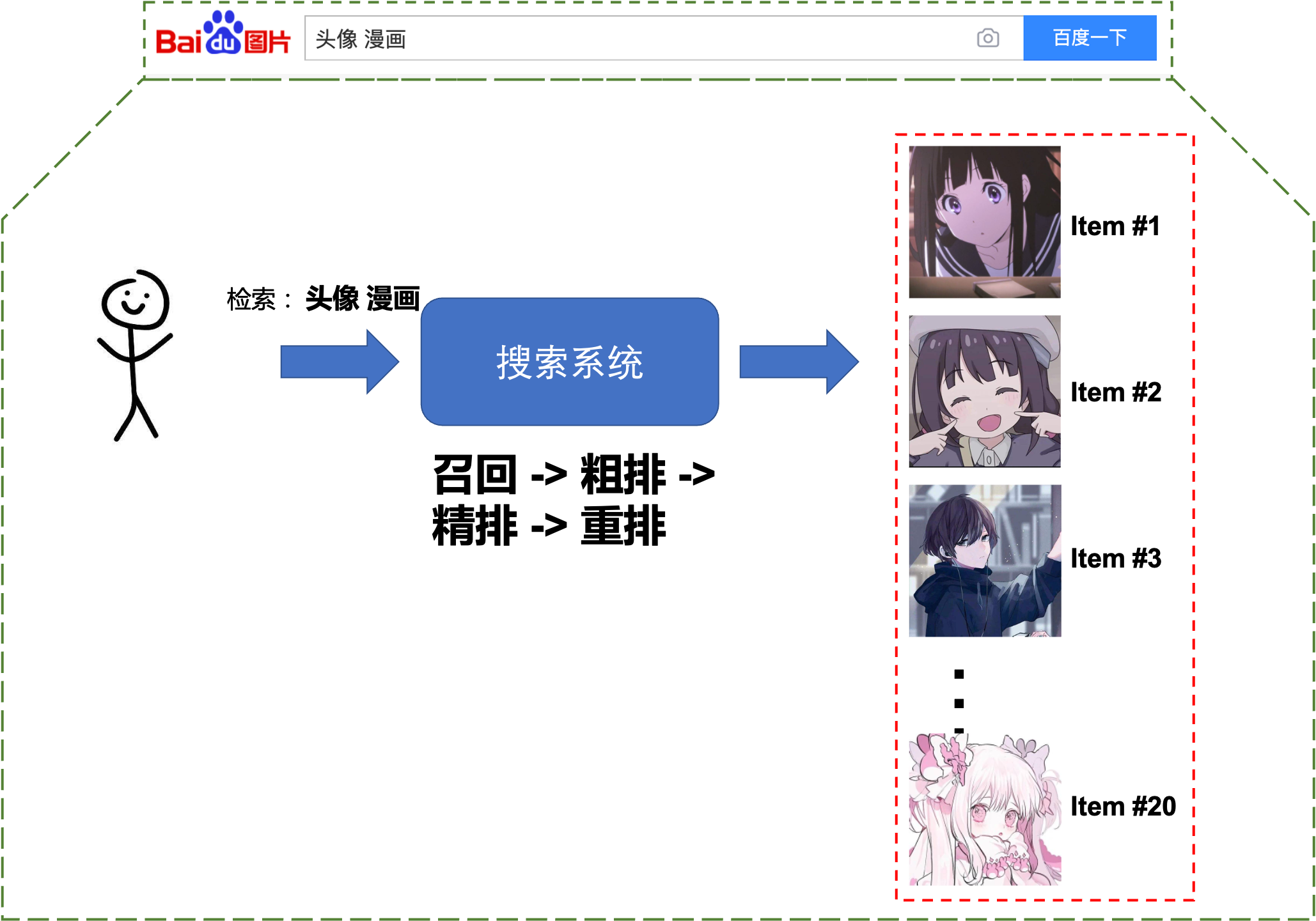
如果从黑盒子的角度去看待搜索系统，那么可以将搜索系统看成是输入用户Query（用户表达需求的手段），搜索系统通过一阵鼓捣，最后输出一个相关Doc的有序列表，如Fig 1.1所示，对搜索系统更为细节的介绍可见 [5]。可以看出『有序』对于搜索系统的重要性，它直接决定了这个搜索系统的性能，而Learning To Rank（LTR）模型就是用于对若干个Doc进行排序的模型，其输入是若干个Doc的特征，而输出是每个Doc的先后顺序。一般而言，理想中的Doc的先后顺序取决与产品定义，以及LTR模型应用在搜索系统的何种阶段，比如在上层排序中可能会考虑到Doc的CTR信号，其排序需求和粗排（大部分时候考虑Query-Doc的相关性，质量性等等）就可能有所区别。关于LTR模型的详细介绍可见综述 [3,4]。

Fig 1.1 搜索系统从黑盒子的角度看，是输入Query，输出相关Doc的有序列表。

为了描述的简单性考虑，本文只考虑相关性排序。那么总得来说，LTR模型对于Doc排序可以有两种方式：

  1. 绝对相关性判断: LTR模型对每个文档给出其相关性判断，通过对这个数值进行排序，从而得到文档有序列表，这类型的模型通常是回归模型，比如GBDT模型。
  2. 相对相关性判断： 对所有文档构建出个有序对，而LTR模型通过对每个有序对进行相关性判断，如果则认为相关性高于，也即是，反之亦然。这种模型包括RankSVM，还有本文将会介绍的GBRank模型等。

绝对相关性判断LTR模型要求每个Doc都有相关性标注，通常需要大量人力进行标注。相对相关性判断LTR模型的标注是有序对的序关系，而不是对Doc的绝对判断，因此获取标注的方式有两种：1. 通过对每个Doc进行人工标注后计算的序关系；2. 通过用户的行为数据（比如点击，停留时长等），从大量的搜索日志中构建出大量有序对数据，从而减少人工标注的压力。注意到，通过人工标注同样可以构建出有序对数据。文章[1]发现，在Doc拥有绝对相关性标注的时候，GBRank通过构建有序对进行训练，性能甚至比单独采用绝对相关性标注进行的GBDT效果还好。我们在介绍完了LTR模型的应用背景后，就开始正式介绍GBRank模型。

GBRank

GBRank [1]全称Gradient Boost Rank模型，其通过采用Gradient Boost Tree模型作为基模型（Base model）对有序对的序关系进行判断，我们之前在 [6]中对GBDT模型进行过简单的介绍，这里为了文章的完整性会再对GBDT模型唠叨几句。我们知道对于一个无约束的多元函数最优化问题，可以通过梯度下降进行求解。假如求解，那么通过梯度下降对参数进行更新的过程为： 其中的为步长，可通过线性查找（Linear Search）在每一步进行求解。在求解多元函数最优值的场景中，函数是已经固定了的，而在回归树的场景中，我们需要求得的最值，不是对参数进行的，而是求得 函数族 的最值。以训练数据为例，我们需要找到一个函数有，如果损失函数为MSE函数，那么有： 其中的为假设的函数族空间，比如整个梯度决策树模型空间。注意到，此时已经不是对参数进行求最优了，而是对整个函数求最优。类似的，函数的梯度下降（functional gradient descent）可以表示为(2-3): 显然我们的训练数据是有限的，因此只能在有限的个训练数据上进行导数计算，也即是： 这样的函数梯度是不完整的，而GBDT模型就采用决策树模型，尝试对函数梯度进行插值。因此，GBDT模型算法可以总结为：

  1. 初始化

  2. 对于个设定的树数量来说，有：

    • 对于个样本，计算负梯度

    • 对于指定的Terminal Region 而言，采用回归树方法对负梯度进行拟合。

  3. 对于，计算 这是对每个Terminal Region进行求平均，具体原因见[6]

  4. 更新函数： 其中的为缩放系数，为指示函数，当条件符合时输出1，否则输出0。

其中的超参数和可通过交叉验证进行挑选。强烈建议读者移步 [6]，有些细节和理论没在本文进行展开。以上对GBDT模型进行了简单介绍，我们开始介绍如何通过GBDT回归树去进行有序对排序。

我们用符号表示比更相关，因此期望，其中表示数据的条数。我们构建出有序对数据： 我们用ranking loss作为损失，那么有： （2-7）式子容易陷入平凡解（也就是求出常数解，），因为，因此只要就能够满足。为了解决这个问题，通过在损失函数中引入一个常数即可，如(2-8) 这一点容易理解，此时将不一定等于0，即便陷入平凡解，仍然会产生梯度让优化继续进行。

然而(2-8)由于涉及到了两个自变量，其优化过程并不容易，文章中通过交替固定某个变量为常数，对另一个变量进行优化来解决。也即是： 可知(2-9)上下两式分别将和当成常数，对另一个变量和求导。当的时候，可知不会产生梯度；当时，可知(2-9)可写成(2-10) 也就是说有，这些之前的base model无法解决的『Bad case』，可以理解为我们函数梯度更新的方向需要使得，这也即是我们下一个迭代的base model需要满足的，可知此时可以将和看成是常数。不妨构建数据: 给下一次迭代的base model进行学习，这也满足Boost范式中逐渐解决上一次迭代未解决的bad case的思想。那么GBRank算法可以总结为：

  1. 对进行初始化

  2. 对于 （base model的数量）有：

    • 用作为对的估计，将分割为两个互斥的集合:

    • 用回归树去对数据进行拟合。

    • 更新为：

构建有序对数据

以上章节讲述了算法的构成，我们还一直没谈如何构建有序对数据。一般来说可以通过两种方式进行构造：1. 从人工标注数据中构造有序对；2. 根据用户行为信号构造有序对。

从人工标注数据中构造

对于某个检索词q和两个文档，有二元对，可以根据相关性（或其他指标，看系统需求）对二元对进行标注，比如有0-4五个档位，用表示和第个文档的标注，那么如果有，就有偏序关系，也就可以构建出有序对。

根据用户行为信号构造

根据用户行为信号（比如点击信号）进行有序对构造，也称为隐式反馈（Implicit Feedback）,论文[2]对从隐式反馈中构建有序数据有过深入研究，而本文也是基于[2]的研究进行的。对于一个检索词q而言，考虑其前10结果中的任意两个文档，其中的文档展现了次，被点击了次；而文档展现了次，被点击了次。那么需要通过假设检验对，对和是否可以视为是通过点击信号，就能判断某个比另一个更好的二元对。假设点击行为符合二值分布，那么有： 作者采用likelihood ratio test (LRT) 进行检验，有： 一旦文档对和通过了假设检验，即可通过论文[2]中提到的Skip-Above等类似的方法构造有序对，Skip-Above可以简单解释如下。假设某次检索的结果，返回了有序的文档列表（其中下标越大表示排序越后）： 其中上标带*的表示是用户点击过了的文档，那么Skip-Above认为排序越后但是被点击过了的文档，其相关性会比排序靠前但是未被点击的文档相关性更好，也就是有 , , 。在本文中，因为可能两个文档都被点击过，不能直接采用Skip-Above 方法。可以考虑对点击次数卡阈值的方法，再采用 Skip-Above进行有序对构造。Skip-Above的产生是有着用户行为学实验和分析的，这个我们后续的博文再进行介绍。

Reference

[1]. Zheng, Zhaohui, et al. "A regression framework for learning ranking functions using relative relevance judgments." Proceedings of the 30th annual international ACM SIGIR conference on Research and development in information retrieval. 2007.

[2]. Joachims, Thorsten, et al. "Accurately interpreting clickthrough data as implicit feedback." Acm Sigir Forum. Vol. 51. No. 1. New York, NY, USA: Acm, 2017.

[3]. Li, Hang. "Learning to rank for information retrieval and natural language processing." Synthesis lectures on human language technologies 7.3 (2014): 1-121.

[4]. Liu, Tie-Yan. "Learning to rank for information retrieval." Foundations and Trends® in Information Retrieval 3.3 (2009): 225-331.

[5]. 从零开始的搜索系统学习笔记, https://blog.csdn.net/LoseInVain/article/details/116377189

[6]. GBDT-梯度提升决策树的一些思考, https://blog.csdn.net/LoseInVain/article/details/113429866