如果给定了计算预算C，如何分配LLM的模型尺寸N和训练的数据量D，才能使得模型的效果L最好呢...

FesianXu 20250304 at Wechat Search Team

前言

如果给定了计算预算，如何分配LLM的模型尺寸和训练的数据量，才能使得模型的效果最好呢？笔者在此介绍一篇经典的文章讨论这个问题。如有谬误请见谅并联系指出，本文遵守CC 4.0 BY-SA版权协议，转载请联系作者并注明出处，谢谢。

关键字：最佳计算预算分配
发表信息：NIPS 2022

联系方式：

e-mail: FesianXu@gmail.com

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

微信公众号：机器学习杂货铺3号店

我们知道在大语言模型（Large Language Model, LLM）中，存在所谓的尺度扩展规律（Scaling Laws） [2]，如Fig 1所示，即是：

LLM的性能会随着模型的参数量、模型的训练量、模型的训练数据量的增加而增加

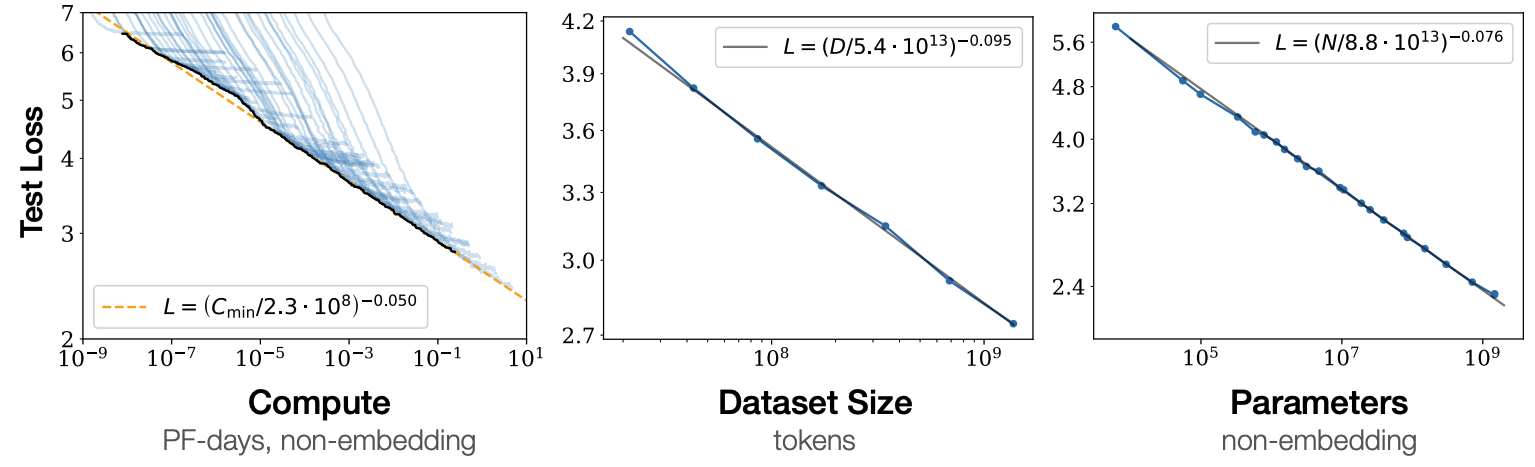
Fig 1. 大模型中的尺度扩展规律，测试集损失随着模型训练量、训练集数据量、模型参数量的增加而递减（即是模型性能递增）。

我们也知道模型的参数量、模型的训练量和模型的训练数据量都会影响到最终的计算预算（可以用FLOPs计算），因此LLM的性能可以说和计算预算直接挂钩，这也是Fig 1 左图所表示的。我们不禁会有个疑问，给定了模型的计算预算，我们应该怎么均衡模型参数量和预训练的Token数量，才能使得模型的预训练损失最小化呢？我们期待得到最优的模型参数和最优的预训练Token数量，可以使得预训练损失最小，正如公式(1)所示。

作者探索这个规律的方法论也很直接，作者步进遍历了一遍不同的模型尺寸（从70M到16B参数量），也步进遍历了一遍预训练数据Token数量（从5B到400B），最终跑了超过400个组合的数据点，不得不说有算力真的可以为所欲为。从直观上看越大尺寸的模型需要越多训练的Token，当然我们需要研究具体的比例，作者采用了三种不同的方法去找这个比例关系。

固定模型尺寸下的性能分析

这种方法是分别固定住模型尺寸（从70M到10B多个模型尺寸都需要实验），然后观察训练了不同数量的Tokens数量后，在每一个节点时哪一个模型尺寸能够达到最小的训练损失。如Fig 2 左图所示，这里有些地方需要解释。首先这里的横坐标是浮点计算量FLOPs，在不同模型尺寸下，相同的FLOPs能训练的Token数量是不同的，因此才会出现Fig 2左图中同一个FLOPs中，大尺寸模型损失比小尺寸模型还大的情况。从Fig 2 左图中，我们能发现在不同的FLOPs下，到达最小损失的模型尺寸是不一样的（不太容易看出来，在左图中是灰色点，它们形成了一个包络线），不同的FLOPs在对应尺寸模型下能够折算成训练过的Token数量，因此能够画出Fig 2 中图和右图，横坐标是FLOPs，纵坐标是达到最小损失（也就是左图的灰色点）时的模型尺寸和过了的Tokens数。换句话说，Fig 2中图和右图就是给定计算预算下的最佳模型尺寸和训练数据量，我们发现有，通过实验可以算出。

Fig 2. 训练曲线包络。左侧展示了我们所有不同的运行情况。我们启动了一系列模型尺寸，从70M到10B，每个模型针对四个不同的余弦循环周期长度。从这些曲线中，我们提取了每 FLOP 最小损失的包络线，我们利用这些点来估计给定计算预算下的最佳模型尺寸（中间）和最佳训练 token 数量（右侧）。绿色显示了基于训练 Gopher（5.76 × 10²³ FLOP）所用 FLOP 数量的最佳模型尺寸和训练 token 数量的预测。

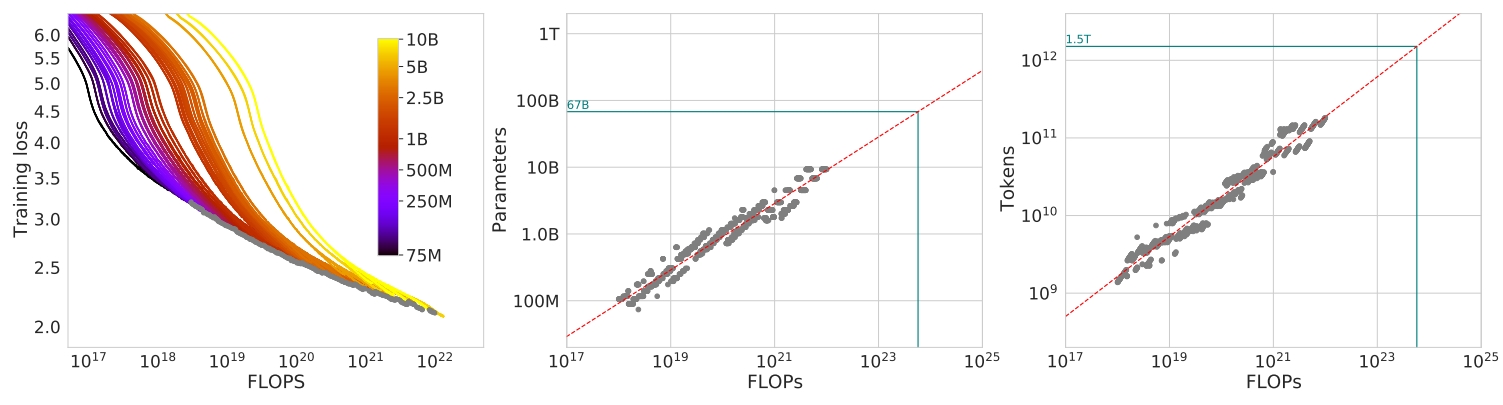
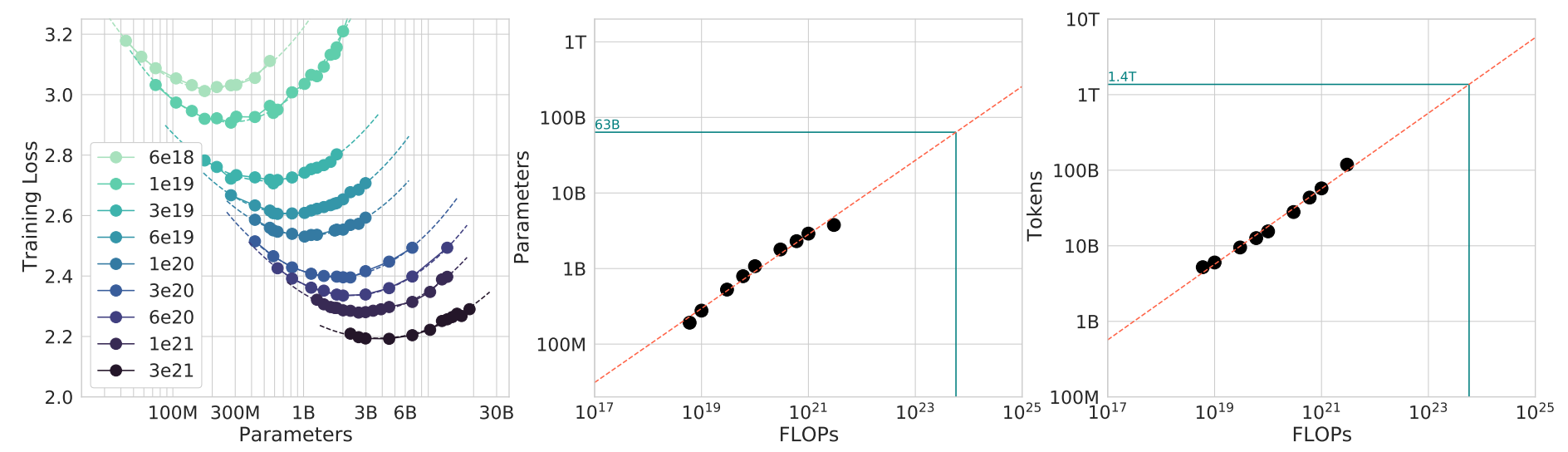
固定计算预算下的性能分析

第一种方法的计算量FLOPs没有固定，在此方法中我们固定计算量（也就是所谓的IsoFLOP），分析等量计算下的最佳模型参数量。同时，在知道了每个实验固定的计算量，和在此之下的最佳模型参数量后，也就可以反推训练Token数量。实验如Fig 3 左图所示，可以发现在不同的固定计算量下（从到 FLOPs），遍历不同尺寸的模型能够发现在某些尺寸处会存在明显的低谷，这个低谷就是在固定计算预算情况下的最佳模型参数量，由此也能绘制出Fig 3 中图和右图，绘制逻辑如第一种方法所述。不难发现同样有这个规律，算出。

Fig 3. 等量浮点运算曲线（IsoFLOP Curves）：针对不同模型规模，通过调整训练令牌（token）数量，使得最终总浮点运算量（FLOPs）保持恒定，并设置余弦周期长度以匹配目标FLOPs量。研究发现，损失函数会出现一个明显低谷（如左图），这表明在给定FLOPs计算预算下，存在一个最优的待训练模型。基于这些低谷位置，我们推算出更大模型的最优参数规模与令牌数量（中图和右图）。图中绿色部分展示了在Gopher模型计算预算下，最优模型的参数与令牌数量估计值。

对参数化损失函数进行拟合

在第1和2中方法中已经积累了很多最小损失下的的数据点了，我们不妨把损失拆解为三大部分如公式(2)所示，其中第一项为不可约损失，也就是自然文本的熵，是不可继续减少的最基础的损失项。第二项为（不完美的）参数量为的Transformer模型训练过程中产生的损失（因为参数量总是有限，也就是不完美的，因此总是在理想损失的基础上有超额损失），第三项则是（不完美的）训练数据量下（因为训练数据量不可能是无限的）的产生的超额损失。

作者采用L-BFGS算法去最小化所谓的Huber loss（因为数据点只有400多个，这个loss作者说对离群点比较稳健）去进行估计，笔者也没细究，读者有兴趣的可以翻阅 [3] 和 [4]。最终估计出来的参数为：在LLM Scaling Law的论文 [2] 中提出了一个估算: ，借此可以将公式(2)进行变形，得到公式(4)

$公式，正体下标公式，的逆其中$

作者算得，具体过程请自行参考原文。

给定计算量下的最优设计

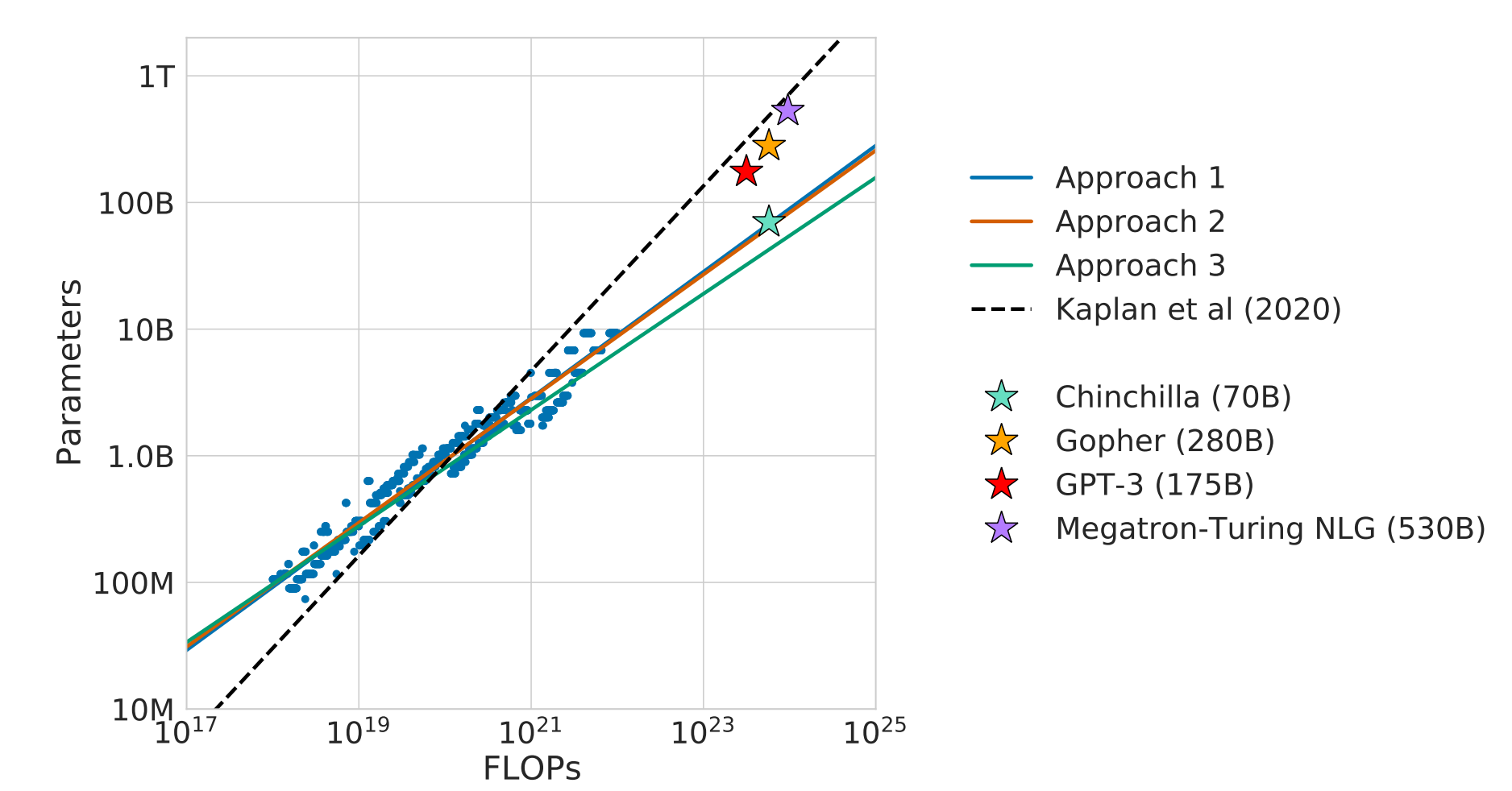
Fig 4是将以上三种预测方法绘制成计算量——最佳模型尺寸估计曲线图，其中那贴上了一些之前工作的估计 [2] 和一些模型的对比，如Gopher（280B参数量）、GPT-3（175B参数量）和Megatron-NLG （530B）参数量。从图中能发现：

方法1和方法2估计出来的曲线基本上贴合，方法3估计出的模型尺寸在计算预算小的时候和前两者基本贴合，但在大计算预算下会偏小些，不过也不会差距特别大。
主流的大模型，如Gopher、GPT3等在对应的计算预算下，模型尺寸明显偏大，基本上是贴着 [2] 的曲线走的。

为了证明本文提出的估计方法更佳准确，作者在方法1和2中对齐Gopher的计算预算（大概是 FLOPs），找到了最佳模型尺寸，约是70B，作者将这个训练出来的模型称之为Chinchilla，需要将这个模型的性能和Gopher进行公平对比。注意到在方法1和2中，从Fig 2和Fig 3的右图中可以找出给定预算下的最佳训练Token数量，对于Chinchilla来说是1.4-1.5T左右，因此。

Fig 4. 预测结果叠加对比：我们将三种不同方法的预测结果与Kaplan等人 [2] 的推算进行叠加对比。研究发现，所有方法均表明，当前大型模型的参数规模应显著缩小，并因此需要比现有实践更长的训练时间。

作者在相当多语言下游任务的基准上进行了测试，都发现Chinchilla对比Gopher存在普遍优势，在一些任务中甚至超过了Megatron-NLG 530B模型。这些实验过于冗长，笔者就不展示细节了。

笔者读后感

这篇论文的意义在于告诉我们，在给定了计算预算下，是存在一个最优的模型尺寸和训练数据量的，他们存在一个比例（），越大的模型就需要越多数据进行训练，才能发挥出模型最优的性能。这篇论文的发表时间比较早，是2022年，现在已经有很多工作证实了在推理中进行复杂策略可以有效提高模型性能 [5,6]，并且这些推理策略同样也存在Scaling Law。这意味着计算预算不仅可以花在预训练上，而且可以花在推理时的Scaling，这也是这篇文章没有考虑到的点。当然，在 [6] 中作者也承认，推理时的Scaling并非是万能的，而是：

推理时计算与预训练计算并非一对一“可互换”。对于模型能力范围内的简单和中等难度问题，或者在推理（实时性）要求较低的情况下，测试时计算可以轻松弥补额外的预训练。然而，对于超出基础模型能力范围的具有挑战性的问题，或者在推理（实时性）要求较高的情况下，预训练可能更有效于提升性能。

也就是说预训练的地位并不是通过推理时的Scaling就可以替代的，预训练中分配一定量的计算预算对于全方面提高LLM的性能是必须的。结合了模型训练、模型推理的更为综合的最优配比，应该是值得去研究的。

Reference

[1]. Hoffmann, Jordan, Sebastian Borgeaud, Arthur Mensch, Elena Buchatskaya, Trevor Cai, Eliza Rutherford, Diego de Las Casas et al. "Training compute-optimal large language models." arXiv preprint arXiv:2203.15556 (2022).

[2]. Kaplan, Jared, Sam McCandlish, Tom Henighan, Tom B. Brown, Benjamin Chess, Rewon Child, Scott Gray, Alec Radford, Jeffrey Wu, and Dario Amodei. "Scaling laws for neural language models." arXiv preprint arXiv:2001.08361 (2020).

[3]. J. Nocedal. Updating Quasi-Newton Matrices with Limited Storage. Mathematics of Computation, 35(151):773–782, 1980. ISSN 0025-5718. doi: 10.2307/2006193. URL https://www.jstor.org/stable/2006193 aka L-BFGS

[4]. P. J. Huber. Robust Estimation of a Location Parameter. The Annals of Mathematical Statistics, 35 (1):73–101, Mar. 1964. ISSN 0003-4851, 2168-8990. doi: 10.1214/aoms/1177703732. URL https://projecteuclid.org/journals/annals-of-mathematical-statistics/volume-35/issue-1/Robust-Estimation-of-a-Location-Parameter/10.1214/aoms/1177703732.full. aka Huber loss

[5]. https://fesianxu.github.io/2025/03/02/test-time-scaling-laws-20250302/，《大模型推理时的尺度扩展定律》

[6]. Snell, Charlie, Jaehoon Lee, Kelvin Xu, and Aviral Kumar. "Scaling llm test-time compute optimally can be more effective than scaling model parameters." arXiv preprint arXiv:2408.03314 (2024).