BoNBoN——结合行为模仿和偏好对齐进行Best-of-N对齐的方法

Posted on | In |
Words count in article: 496k 字 | Reading time ≈ 30:05 分钟

BoNBoN结合了行为模仿和偏好对齐，在模型的Best-of-N结果基础上进行对齐...

FesianXu 20250314 at Wechat Search Team

前言

这次笔者想要介绍的论文，其结合了行为模仿和偏好对齐，在模型的Best-of-N结果基础上进行对齐，具有一定的启发性。论文中有不少公式推导，笔者将会考虑行文整体流畅情况下，酌情引用。如有谬误请见谅并联系指出，本文遵守CC 4.0 BY-SA版权协议，转载请联系作者并注明出处，谢谢。

  • 关键词：行为模仿、偏好对齐、Best-of-N

联系方式：

e-mail: FesianXu@gmail.com

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

微信公众号：机器学习杂货铺3号店

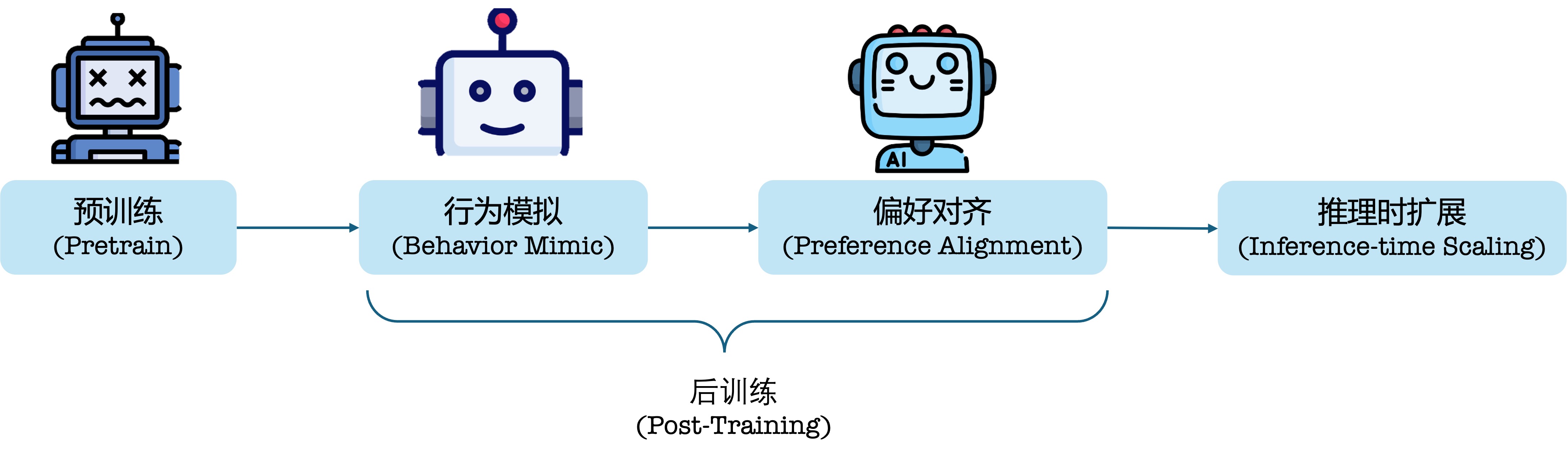
典型的大模型管道可以分为如Fig 1所示的几部分，其中的行为模拟（Behavior Mimic）通常是通过指令微调（Supervised Fintune, SFT）的方式，使得模型可以从预训练后的续写模型，变为一个可以遵循用户指令进行回答的模型，通过偏好对齐（Preference Alignment）能够使得回答更具有人类偏好。存在不少工作认为行为模拟只是对模型回答的格式进行规范，是一种偏向于『记忆（Memorize）』的过程 [2,3]，而偏好对齐才是能进一步提高模型泛化能力的关键 [3]。至于说到推理时扩展（Inference-time Scaling），则是考虑在推理阶段采用复杂的答案采样/答案改写方式，提升模型的最终性能，可参考笔者在博文 [4] 中的介绍。

Fig 1. 典型的大模型训练和推理管道。

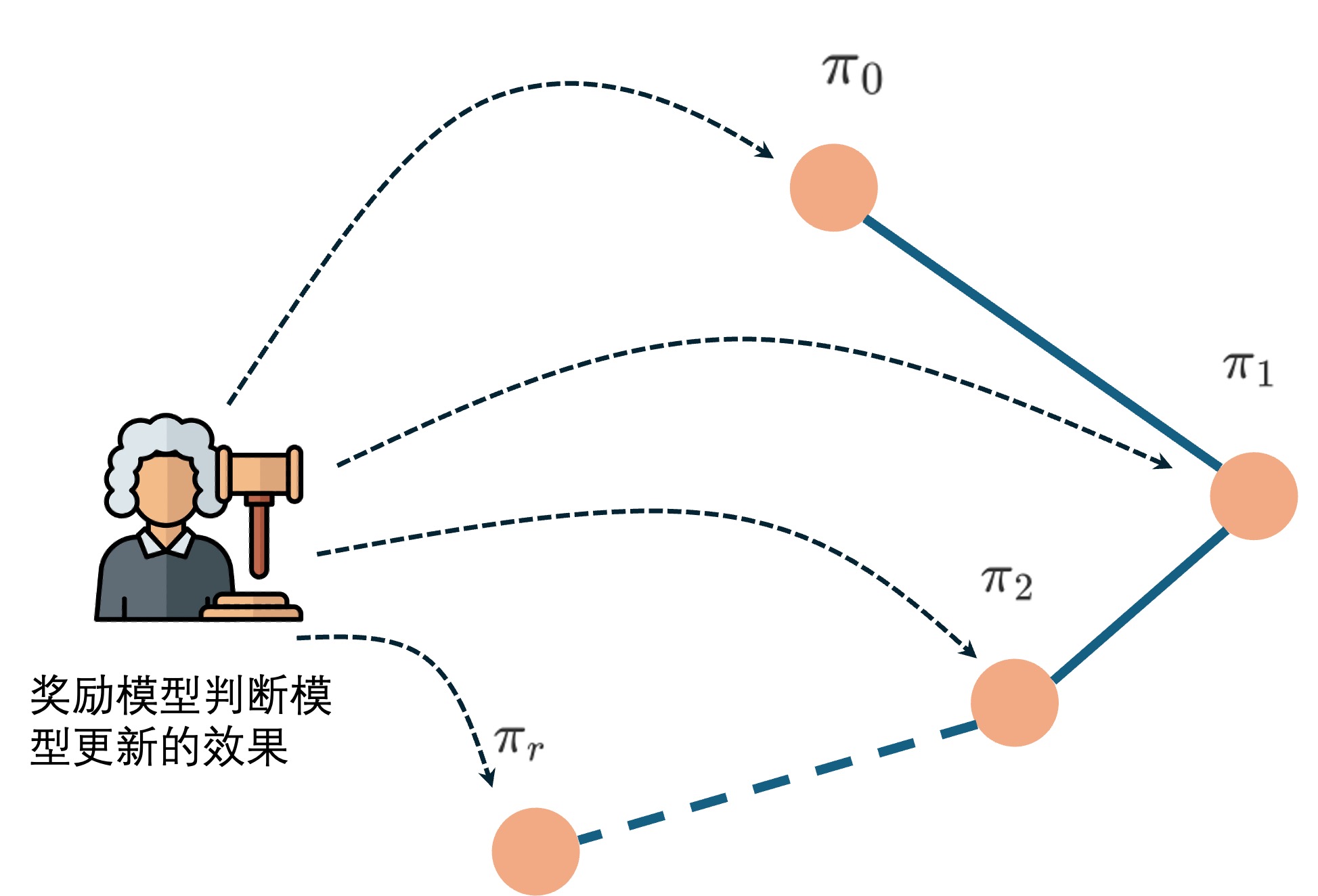
Best-of-N （下文简称BoN）采样是推理时扩展的一种经典做法，指的是给定一个提示词， 大模型对其进行采样次，得到个完整回答，通过奖励模型分别打分得到个奖励打分，取其打分最高的作为BoN结果。整个过程可以表示为公式 (1) 所示 作者在文中证明了BoN结果是考虑了KL散度约束情况下的渐进最优策略，在论文 [5] 中同样进行了这一点的证明，整个过程比较复杂，笔者也没完全看懂，尽量挑一些关键结论和过程进行解释。

首先我们看到偏好对齐，偏好对齐的目标是对于一个SFT后的模型，称之为，我们希望学习出一个新模型，应该在某个指标层面上要优于。为了使得训练过程可控，我们也不希望太过远离，可以考虑用KL散度去度量这两者的距离，其中为给定了提示词情况下的KL散度，而则是对提示词集合进行求期望得到的KL散度。KL散度取值范围为，越小表示两个分布之间差别越小。

一种可以考虑衡量优于的指标是胜率（win-rate），定义如下公式（3）所示，也就是通过奖励函数去判断优于的概率。 不妨可以将偏好对齐看成是一个探索&利用（Explore and Exploit）的过程，如Fig 2所示，消耗KL散度距离衡量和初始模型的偏离程度，可以认为是探索程度，用奖励模型新探索的模型进行评估，则可看成是利用过程。因此KL距离是一种可消耗的资源，这个观点在一些工作中也有所体现，可参考 [6]。为何不希望新策略太过于偏离初始策略呢？笔者的理解是：

  1. 如果不在训练过程中对此进行约束，新策略可能会容易出现大幅度偏离初始策略，导致整个训练过程不稳定且难以控制。
  2. 奖励模型通常是在初始策略模型的基础上，采样后进行人工标注样本训练得到的，也就是说如果新策略模型太过于远离初始策略模型，那么很可能会出现奖励模型无法很好地衡量新策略模型效果的情况，从而导致过拟合。

Fig 2. 在偏好对齐过程中，通过消耗KL距离探索新策略模型，而奖励模型作为『法官』进行效果判断。

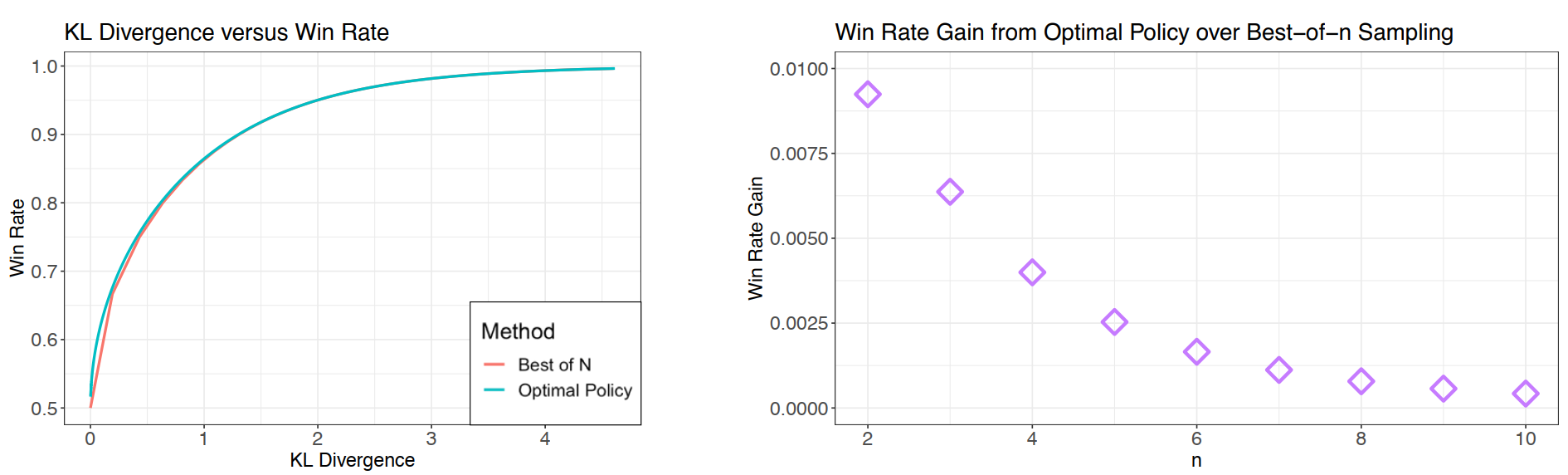
偏好对齐的方法整体有两种，第一个通过人工反馈的强化学习方法（RLHF），如公式（4）所述； 第二种则是通过对比式方法（Contrastive methods），典型的如DPO方法，如公式（5）所示。 RLHF方式显式地引入KL散度约束项，而DPO方法则通过新策略模型分布和初始策略模型分布进行比较的方式，都一定程度上约束了新策略模型不至于偏离初始策略模型。如果奖励模型是Bradley-Terry模型，那么有： 作者文中说因此RLHF和DPO的解析解则可以表示为（对此，笔者不知道具体推导过程，望请教）： 也就是说新策略模型是对初始策略模型的加权，而权值会收到奖励模型的影响。作者认为不仅对于RLHF和DPO，对于包括BoN方式在内的一切对齐策略来说，存在统一的表达，即是有： 其中的是一个非减函数，会收到不同提示词的影响。基于此，可以推导出BoN方式的胜率为（具体过程参考原论文）: 那么最优策略的胜率如何呢？首先我们定义最优策略，就是在给定的KL散度情况下能取得尽可能高的胜率，如公式（10）所示： 此时可以推导出最优策略模型为： 那么最优策略的胜率可以表示为 如果对BoN和最优策略分别绘制曲线图的话，如Fig 3所示，会发现BoN方式是在有KL散度约束下的渐进的最优策略。

Fig 3. 就胜率与KL散度的关系而言，BoN本质上与最优策略表现一致。就胜率与KL散度的关系而言，BoN本质上与最优策略表现一致。 左图：BoN与最优策略的胜率随KL散度变化曲线。右图：不同n值下最优策略与BoN策略的胜率差异。

那么问题来了，如何将模型的BoN的结果蒸馏到模型自身上呢？本文提出了BoNBoN方式，损失函数如公式（13）所示 损失的第一项为SFT损失，其为BoN结果，显然这种方法只是采用了BoN结果作为模仿目标，并没有充分利用数据，比如Worst-of-N（WoN）部分的数据。 而损失的第二项是一个对比式的损失IPO（是DPO的升级，添加了正则项减少过拟合），关于这里的正则项文中附录有推导，博文就不赘述了。IPO-BoN损失不仅采用了BoN结果作为正向样本（也就是），还采用了WoN结果作为负向样本（也就是），数据的利用率更高。 其中 在实验部分，作者比较了Summarization和helpful and Harmless这两块任务，如Fig 4.所示，其中的黑线（BoN theoretical）是根据公式（9）绘制出来的，而BoN Sampling则是真实采样得到的结果，可以发现是能够符合曲线的。我们看这个图，应该从两个维度看：

  1. 胜率越高，说明相比初始策略模型效果更好
  2. 越接近Reference Model（无论是KL散度还是平均响应长度），说明消耗的KL距离越少，则是更占优势（笔者认为是胜率计算更加准确）

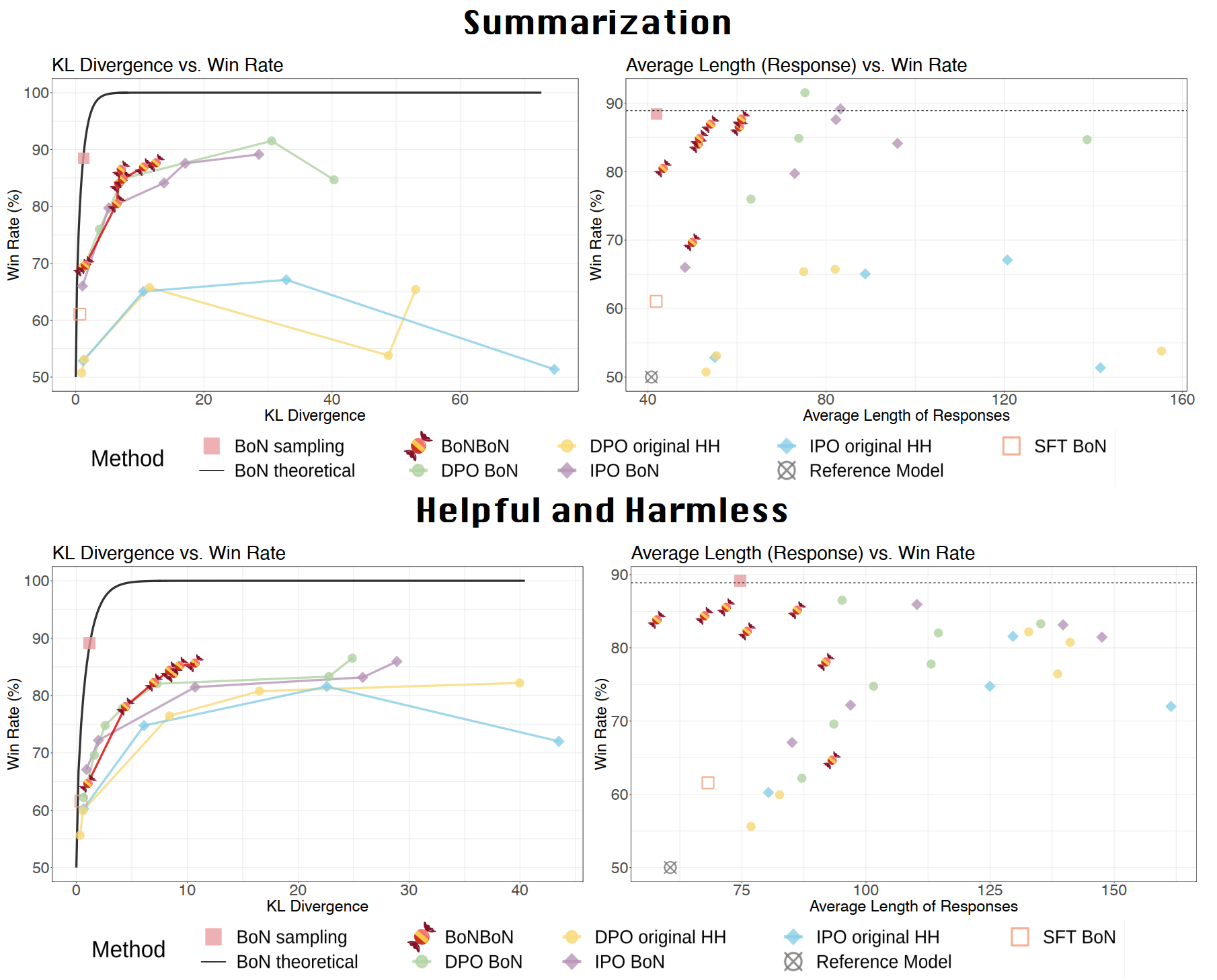
从这个分析角度看，我们发现BoNBoN方法在消耗更少KL距离（或者和初始策略模型更加接近长度的平均响应长度）的情况下，能取得更高的胜率。此外，我们看到DPO BoN 效果持续远远优于DPO original HH，后者是采用HH数据（也就是所谓的off-policy的数据），而前者则来自于模型自身的BoN结果组建偏序数据，也就是所谓的on-policy数据。从这个结果，我们得到一个结论是，应当尽可能采用on-policy数据进行模型偏好对齐，即便这些结果可能相对来说比较弱（对比其他更好的模型采样或者标注）。

Fig 4. BoNBoN在实现高胜率的同时，对生成过程中非目标方面的影响极小（也就是偏离初始策略模型的程度）。每个数据点代表采用特定对齐方法的模型，我们使用一个Ranker测量其相对于基础模型的胜率。为评估非目标行为的改变，我们同时测量了估计的KL散度（左图）和平均响应长度（右图）。上方：BoNBoN与基线模型在摘要任务中的对比结果。下方：BoNBoN与基线模型在单轮对话任务中的对比结果。

读后感

笔者看完这篇文章后，第一感觉就是公式好多... 其实整个蒸馏BoN结果的思路很直接，就是在SFT的基础上添加了一个DPO类的损失（或者反过来说，在DPO偏好对齐的基础上加了一个SFT行为模仿），其实整篇文章很多篇幅在证明BoN是KL约束下的渐进最优策略，然后想办法去接近BoN。因此我总结从这篇文章得到的收获的话：

  1. BoN是LLM的KL约束限制下的渐进最优策略
  2. 新策略模型可以表示为初始策略模型的分布加权
  3. on-policy vs off-policy 数据作为偏好对齐，应当尽可能采用前者
  4. SFT+DPO类损失能够更加充分利用数据

Reference

[1]. Gui, Lin, Cristina Gârbacea, and Victor Veitch. "Bonbon alignment for large language models and the sweetness of best-of-n sampling." arXiv preprint arXiv:2406.00832 (2024). aka BoNBoN

[2]. Zhou, Chunting, Pengfei Liu, Puxin Xu, Srinivasan Iyer, Jiao Sun, Yuning Mao, Xuezhe Ma et al. "Lima: Less is more for alignment." Advances in Neural Information Processing Systems 36 (2023): 55006-55021. aka LIMA

[3]. Chu, Tianzhe, Yuexiang Zhai, Jihan Yang, Shengbang Tong, Saining Xie, Dale Schuurmans, Quoc V. Le, Sergey Levine, and Yi Ma. "Sft memorizes, rl generalizes: A comparative study of foundation model post-training." arXiv preprint arXiv:2501.17161 (2025).

[4]. 《大模型推理时的尺度扩展定律》, https://fesianxu.github.io/2025/03/02/test-time-scaling-laws-20250302/

[5]. Yang, Joy Qiping, Salman Salamatian, Ziteng Sun, Ananda Theertha Suresh, and Ahmad Beirami. "Asymptotics of language model alignment." In 2024 IEEE International Symposium on Information Theory (ISIT), pp. 2027-2032. IEEE, 2024.

[6]. 《奖励模型中的尺度扩展定律和奖励劫持》, https://fesianxu.github.io/2025/02/09/scaling-law-in-reward-model-20250209/