也许一文能够看懂的DPO和PPO方法...
前言
大模型基础教程类的文章,这篇鸽了好些时间了,终于抽时间写完了,希望对大家有帮助。如有谬误请见谅并联系指出,本文遵守CC 4.0 BY-SA版权协议,转载请联系作者并注明出处,谢谢。
e-mail: FesianXu@gmail.com
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号:机器学习杂货铺3号店

偏好对齐
典型的大语言模型(Large Language Model,LLM)管道可以分为如Fig 1.1所示的几部分,其中的行为模拟(Behavior Mimic)通常是通过指令微调(Supervised FineTune, SFT)的方式,使得模型可以从预训练后的续写模型,变为一个可以遵循用户指令进行恰当格式回答的模型,通过偏好对齐(Preference Alignment)能够使得回答更符合人类价值观、意图及特定任务需求。
存在不少工作认为行为模拟只是对模型回答的格式进行规范,是一种偏向于『记忆(Memorize)』的过程 [2,3],而偏好对齐才是能进一步提高模型泛化能力的关键 [3]。至于说到推理时扩展(Inference-time Scaling),则是考虑在推理阶段采用复杂的答案采样/答案改写方式,提升模型的最终性能,可参考笔者在博文 [4] 中的介绍。
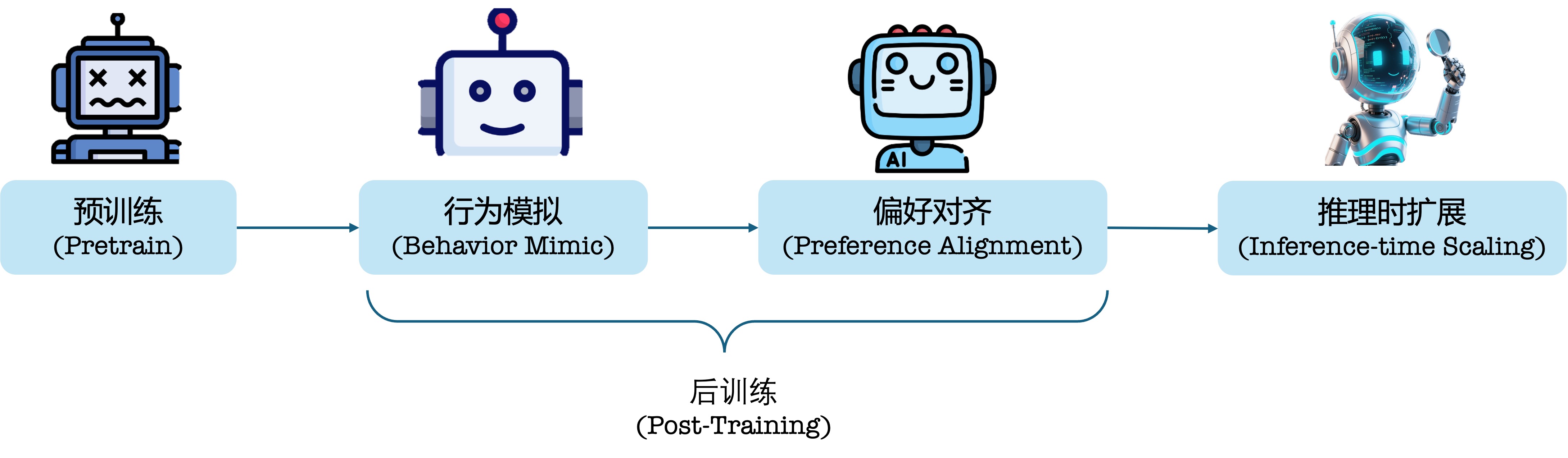
预训练过程本质上是减少策略模型(Policy Model)的搜索空间,将搜索空间限制在目标区域内(比如人类的自然语言和语义范围内),而行为模拟是通过人类给出<问题, 回答>的示例对,给LLM去学习给定了特定任务下的预期回答,相当于是只给定了回答的正例,没有告诉LLM什么样的答案是不可接受的(负例)。此时如果LLM对于训练集外的问题尝试回答,新产生的样本可能会落在负例的区域,表现出来的就是回答出现不符合人类偏好的特性,比如缺失关键信息、出现违反道德法律的内容等等。
一个自然的做法就是提供负例,以三元组<问题, 正例回答, 负例回答>的形式,同时告诉模型哪类型的回答是可接受的,哪类型的回答是不可接受的,这种同时提供正例负例的方式,也可以称之为对比式对齐(Contrastive Alignment)。此处的正例和负例,如果都来自于策略模型本身的采样,那么称之为在轨策略(on-policy),如果其中某个来自于其他模型(比如GPT4)的修正,或者人工标注等非策略模型本身,那么称之为离轨策略(off-policy)。一种常用的正例和负例采样方式,如Fig1.2所示,是采用奖励模型对策略模型的
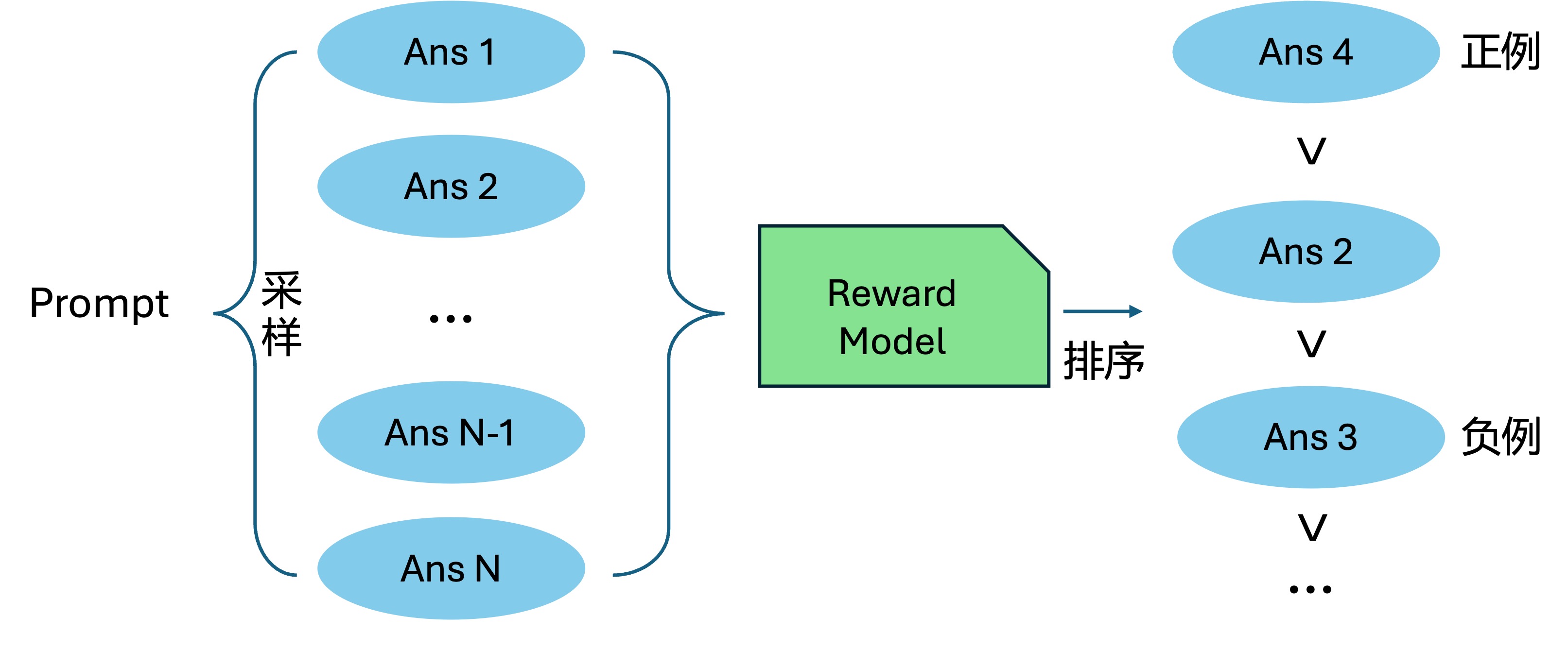
采样出来了正负例后,一种直观的做法是优化公式(1-1),其中的

因此,一个合理的做法是对(1-1)进行约束,尽可能让策略模型『步步为营』,让策略模型在更新过程中,不要偏离初始模型
我们可以用简单的python代码解释DPO的流程:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63import torch
import torch.nn.functional as F
from transformers import AutoModelForCausalLM, AutoTokenizer
# 示例数据集结构
# 设数据集为三元组(prompt, chosen_response, rejected_response):
# preference_data = [
# {"prompt": "解释量子力学", "chosen": "量子力学是...", "rejected": "量子力学是魔法"},
# {"prompt": "写一首诗", "chosen": "春风拂面...", "rejected": "今天天气..."}
# ]
class DPOTrainer:
def __init__(self, model_name, ref_model_name, beta=0.1, lr=1e-5):
# 初始化当前策略模型和参考模型(冻结参数)
self.model = AutoModelForCausalLM.from_pretrained(model_name)
self.ref_model = AutoModelForCausalLM.from_pretrained(ref_model_name).eval()
self.tokenizer = AutoTokenizer.from_pretrained(model_name)
self.optimizer = torch.optim.AdamW(self.model.parameters(), lr=lr)
self.beta = beta
def get_logprobs(self, model, input_ids, attention_mask):
# 计算给定输入的log概率
with torch.set_grad_enabled(model.training):
outputs = model(input_ids, attention_mask=attention_mask)
logits = outputs.logits
logprobs = F.log_softmax(logits, dim=-1)
return logprobs.gather(-1, input_ids.unsqueeze(-1)).squeeze(-1)
def dpo_loss(self, batch):
# 编码输入
prompt = self.tokenizer(batch["prompt"], return_tensors="pt", padding=True)
chosen = self.tokenizer(batch["chosen"], return_tensors="pt", padding=True)
rejected = self.tokenizer(batch["rejected"], return_tensors="pt", padding=True)
# 计算策略模型和参考模型的log概率
with torch.no_grad():
ref_chosen_logp = self.get_logprobs(self.ref_model, chosen.input_ids, chosen.attention_mask).sum(-1)
ref_rejected_logp = self.get_logprobs(self.ref_model, rejected.input_ids, rejected.attention_mask).sum(-1)
policy_chosen_logp = self.get_logprobs(self.model, chosen.input_ids, chosen.attention_mask).sum(-1)
policy_rejected_logp = self.get_logprobs(self.model, rejected.input_ids, rejected.attention_mask).sum(-1)
# 计算损失
log_ratio_chosen = policy_chosen_logp - ref_chosen_logp
log_ratio_rejected = policy_rejected_logp - ref_rejected_logp
loss = -F.logsigmoid(self.beta * (log_ratio_chosen - log_ratio_rejected)).mean()
return loss
def train_step(self, batch):
self.model.train()
loss = self.dpo_loss(batch)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
return loss.item()
# 示例训练流程
trainer = DPOTrainer("Qwen", "Qwen") # 假设参考模型为预训练Qwen
for epoch in range(10):
for batch in dataloader:
loss = trainer.train_step(batch)
print(f"Epoch {epoch}, Loss: {loss:.4f}")
由于DPO这种方式一般会离线准备好成对的偏好数据,我们称之为离线(offline)的偏好对齐方式。
在线采样和对齐
我们观察,然后我们行动
对比式的偏好对齐,每次只能利用成对的偏好数据,假如对于输入
还是看到公式(1-3),由于LLM作为语言模型本身的离散性质(生成的文本的解码过程无法求导),这个公式是无法直接求导的,因此也无法直接优化,那么就需要采用强化学习进行优化,比如近端策略优化(Proximal Policy Optimization, PPO),这也是本博文的主角。公式(1-3)无法求导,那么我们就退而求其次,对于一个输入
注意到这是一个不严谨并且简化后的表示方法,由于LLM的输出通常会具有多个Token,产出每一个Token可以视为是基于之前的产出序列(也就是Actor。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47actor_model = build_actor()
optimizer = build_optimizer()
for episode in range(num_episodes):
for rand_prompts, labels in prompts_dataloader:
# step1: 对每个prompt,都采样得到N个回答,并且计算优势
experiences = make_experience_list(rand_prompts, labels)
# rand_prompts 采样得到的prompt x
# experiences.sequences 采样得到的回答y_t
# experiences.action_log_probs 采样得到回答的策略模型\pi_{\theta}的logprob
# experiences.base_action_log_probs 采样得到回答的参考模型\pi_{ref}的logprob
# experiences.advantages 该回答的优势A_t
# step2: 训练 Actor模型,最多更新max_epochs轮
experiences_dataloader = DataLoader(experiences)
for epoch in range(self.max_epochs):
for experience in experiences_dataloader:
loss = compute_actor_loss(actor_model, experience, **generate_kwargs)
loss = loss.mean()
loss.backward() # 计算梯度
optimizer.update() # 根据梯度,此时更新actor模型参数
def make_experience_list(rand_prompts, labels):
experiences = []
# 采样出N个输出samples_list
samples_list = generate_samples(rand_prompts, labels, **generate_kwargs)
for sample in samples_list:
actor_model.eval()
action_log_probs = actor_model(sample.sequences)
expr = Experience(action_log_probs=action_log_probs)
experiences.append(expr)
return experiences
def compute_actor_loss(actor_model, experience):
action_log_probs, output = actor_model(experience.sequences)
old_action_log_probs = experience.action_log_probs
actor_loss = policy_loss(action_log_probs, old_action_log_probs)
loss = actor_loss
return loss
def policy_loss(log_probs, old_log_probs, advantages):
ratio = (log_probs - old_log_probs).exp()
surr1 = ratio * advantages
surr2 = ratio.clamp(1 - self.clip_eps, 1 + self.clip_eps) * advantages
loss = -torch.min(surr1, surr2)
loss = masked_mean(loss, action_mask, dim=-1).mean()
return loss
注意到在policy_loss中,通过对公式(2-3)取对数,可以将除法转换成减法,如公式(1-1)所示。
估计每个采样回答的优势
如何计算每个采样答案的优势呢?这是PPO算法的核心和难点,首先我们看到优势应该具有什么特性。首先,
我们回过头来解释公式(2-5),
| 概念 | 奖励/收益 | 回报 | 状态价值函数 | 动作价值函数 | 优势 |
|---|---|---|---|---|---|
| 符号表示 | |||||
| 术语 | Reward | Return | State-Value function | Action-Value function | Advantage |
| 含义 | 在状态 | 从当前时刻 | 策略 | 策略 | 策略 |
| 关系 |
显然,我们希望每一个动作
由于当前的策略
还有一种方法称之为时序差分(Temporal Difference, TD),是一种自举式的估计方法,简单来说可以通过后继各个状态的价值估计来更新当前某个状态的价值估计值,这是一个递归的过程。这种方法的特点是有偏,但是低方差。如果说蒙特卡洛采样的目标是通过采样知道当前轨迹的真实回报
因为其目的是通过下一步的价值函数去估计当前的价值函数 ,也就是通过
以上内容是传统强化学习的知识,有兴趣的读者需要翻阅《强化学习》一书了解相关的细节。让我们回到主题,在实际应用中,可以通过广义优势估计(Generalized Advantage Estimation, GAE)[6] 估计优势,GAE结合了蒙特卡洛采样MC和时序差分TD,用于平衡估计过程中的偏差(bias)和方差(variance)。如公式(2-8)所示:
其中的1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58# 源码来自openRLHF
def get_advantages_and_returns(
self,
values: torch.Tensor,
rewards: torch.Tensor,
action_mask: torch.Tensor,
gamma: float,
lambd: float,
) -> Tuple[torch.Tensor, torch.Tensor]:
"""Function that computes advantages and returns from rewards and values.
Calculated as in the original PPO paper: https://arxiv.org/abs/1707.06347
Note that rewards may include a KL divergence loss term.
Advantages looks like this:
Adv1 = R1 + γ * λ * R2 + γ^2 * λ^2 * R3 + ...
- V1 + γ * (1 - λ) V2 + γ^2 * λ * (1 - λ) V3 + ...
Returns looks like this:
Ret1 = R1 + γ * λ * R2 + γ^2 * λ^2 * R3 + ...
+ γ * (1 - λ) V2 + γ^2 * λ * (1 - λ) V3 + ...
Input:
- values: Tensor of shape (batch_size, response_size)
- rewards: Tensor of shape (batch_size, response_size)
Output:
- advantages: Tensor of shape (batch_size, response_size)
- returns: Tensor of shape (batch_size, response_size)
"""
if isinstance(values, list):
# packing samples
# TODO: this is slow...
advantages = []
returns = []
for v, r in zip(values, rewards):
adv, ret = self.get_advantages_and_returns(v.unsqueeze(0), r.unsqueeze(0), action_mask, gamma, lambd)
advantages.append(adv.squeeze(0))
returns.append(ret.squeeze(0))
return advantages, returns
lastgaelam = 0
advantages_reversed = []
response_length = rewards.size(1)
# Mask invalid responses
if action_mask is not None:
values = action_mask * values
rewards = action_mask * rewards
for t in reversed(range(response_length)):
nextvalues = values[:, t + 1] if t < response_length - 1 else 0.0
delta = rewards[:, t] + gamma * nextvalues - values[:, t]
lastgaelam = delta + gamma * lambd * lastgaelam
advantages_reversed.append(lastgaelam)
advantages = torch.stack(advantages_reversed[::-1], dim=1)
returns = advantages + values
return advantages.detach(), returns
行动者-批评者模型
在get_advantages_and_returns这个函数中,rewards通过奖励模型计算得到,那么values应该如何计算得到呢?PPO是一个所谓的行动者-批评者模型(Actor-Critic Model),行动者(Actor)用于学习策略, 批评者(Critic)则进行状态价值函数
- 行动者模型采样,生成一系列待评估的轨迹,这个过程称之为rollout。
- 奖励模型对轨迹进行打分得到
- 当然,第二步对批评者模型是准确的假设是太过于理想了,显然批评者也需要随着行动者模型的训练,而跟着一起迭代。在第二步我们已经知道了在批评者固定的情况下,一直迭代行动者模型,整体价值能到达何种程度(
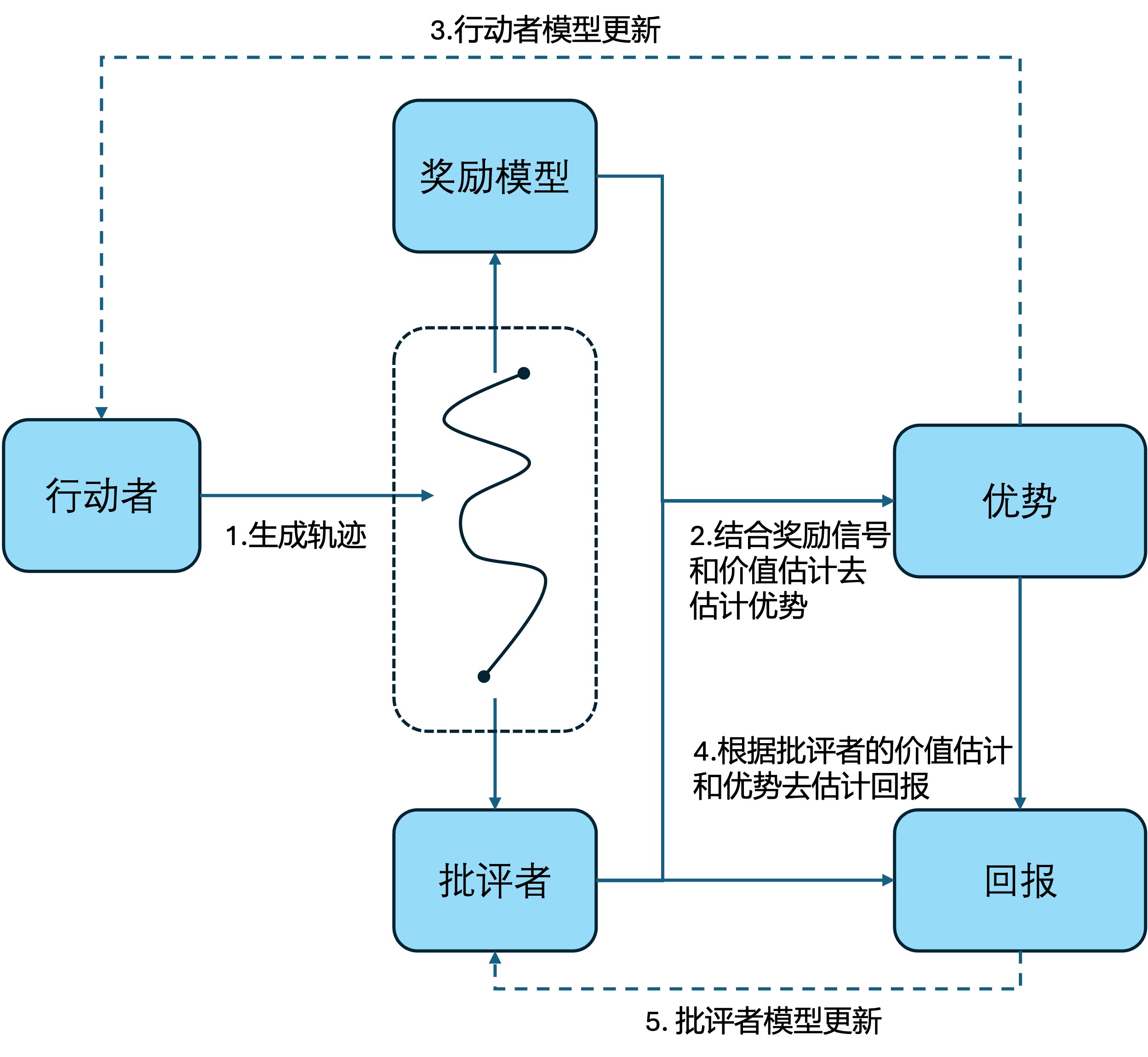
我们不禁要问,为何要用批评者模型去估计当前行动者模型的效果呢?通过奖励模型难道不已经对当前rollout的结果进行了评估了吗?其实这还是短期奖励和长期奖励的区别,奖励模型有几个『毛病』:
- 在PPO训练过程中,奖励模型是固定的,并不会随着训练过程而更新。
- 奖励模型只负责对当前rollout出来的单条回答,逐个进行效果评估,这意味着单个奖励是非常『局部』的——他只能看到样本级别,而且很容易存在方差大的问题,如果将奖励直接当成是对行动者模型的能力判断,从而引导行动者模型训练,那么就很可能导致训练过程的不稳定。
出于这两点考虑,在PPO训练过程中,我们采用一个独立的模型(通常是和行动者模型同质的,甚至是底座完全一样的模型)作为批评者,批评者的建模目标是长期奖励,这意味着批评者的价值评价粒度不只是单个样本级别了,而是整体了。那么,完整的PPO流程的伪代码修改为如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83actor_model = build_actor() # 行动者模型,进行策略采样
critic_model = build_critic() # 批评者模型,进行价值估计
reward_model = build_reward_model() # 进行Reward打分
ref_model = actor_model.clone().detach() # 初始的策略模型作为参考模型
optimizer = build_optimizer()
for episode in range(num_episodes):
for rand_prompts, labels in prompts_dataloader:
# step1: rollout阶段,对每个prompt,都采样得到N个回答
experiences = make_experience_list(rand_prompts, labels)
# rand_prompts 采样得到的prompt x
# experiences.sequences 采样得到的回答y_t
# experiences.action_log_probs 采样得到回答的策略模型\pi_{\theta}的logprob
# experiences.base_action_log_probs 采样得到回答的参考模型\pi_{ref}的logprob
# experiences.advantages 该回答的优势A_t
experiences_dataloader = DataLoader(experiences)
for epoch in range(self.max_epochs):
for experience in experiences_dataloader:
# step2: 训练Actor模型,对于一次rollout的结果集合,进行max_epochs次迭代。
actor_model.train()
critic_model.eval()
actor_loss = compute_actor_loss(actor_model, experience, **generate_kwargs)
actor_loss = actor_loss.mean()
actor_loss.backward() # 计算梯度
optimizer.update() # 根据梯度,此时更新actor模型参数
# step3: 训练Critic模型
critic_model.train()
value = critic_model(sample.sequences)
critic_loss = value_loss(value, experience.returns)
critic_loss = critic_loss.mean()
critic_loss.backward() # 计算梯度
optimizer.update() # 根据梯度,此时更新critic模型参数
def make_experience_list(rand_prompts, labels):
experiences = []
# 采样出N个输出samples_list
samples_list = generate_samples(rand_prompts, labels, **generate_kwargs)
# 奖励函数计算,估计Value,计算kl散度
for sample in samples_list:
actor_model.eval()
action_log_probs = actor_model(sample.sequences)
base_action_log_probs = ref_model(sample.sequences)
value = critic_model(sample.sequences)
reward = reward_model(sample.sequences)
kl = compute_approx_kl(action_log_probs, base_action_log_probs)
expr = Experience(
action_log_probs=action_log_probs,
base_action_log_probs=base_action_log_probs,
value=value,
reward=reward,
kl=kl)
experiences.append(expr)
# 计算优势
rewards = [r['reward'] for r in experiences]
for experience, reward in zip(experiences, rewards):
experience.advantage, experience.returns = get_advantage_and_returns()
return experiences
def compute_actor_loss(actor_model, experience):
action_log_probs, output = actor_model(experience.sequences)
old_action_log_probs = experience.action_log_probs
actor_loss = policy_loss(action_log_probs, old_action_log_probs)
loss = actor_loss
return loss
def policy_loss(log_probs, old_log_probs, advantages):
ratio = (log_probs - old_log_probs).exp()
surr1 = ratio * advantages
surr2 = ratio.clamp(1 - self.clip_eps, 1 + self.clip_eps) * advantages
loss = -torch.min(surr1, surr2)
loss = masked_mean(loss, action_mask, dim=-1).mean()
return loss
def value_loss(values, returns, clip_eps):
loss = (values - returns) ** 2
loss = 0.5 * loss
return loss.mean()
注意,这个伪代码不是真实PPO训练过程中的完整流程,只能提供一个粗略的参考。在真实的流程中,可能还会添加一些约束,比如通过KL loss去约束策略模型(Actor Model)不至于和参考模型(Reference Model)远离太远,保证训练过程的稳定性。但这些都不算是PPO的必备步骤,所以我们就不在这里讨论了。
Reference
[1]. https://github.com/OpenRLHF/OpenRLHF
[2]. Zhou, Chunting, Pengfei Liu, Puxin Xu, Srinivasan Iyer, Jiao Sun, Yuning Mao, Xuezhe Ma et al. "Lima: Less is more for alignment." Advances in Neural Information Processing Systems 36 (2023): 55006-55021. aka LIMA
[3]. Chu, Tianzhe, Yuexiang Zhai, Jihan Yang, Shengbang Tong, Saining Xie, Dale Schuurmans, Quoc V. Le, Sergey Levine, and Yi Ma. "Sft memorizes, rl generalizes: A comparative study of foundation model post-training." arXiv preprint arXiv:2501.17161 (2025).
[4]. 《大模型推理时的尺度扩展定律》, https://fesianxu.github.io/2025/03/02/test-time-scaling-laws-20250302/
[5]. Rafailov, Rafael, Archit Sharma, Eric Mitchell, Christopher D. Manning, Stefano Ermon, and Chelsea Finn. "Direct preference optimization: Your language model is secretly a reward model." Advances in Neural Information Processing Systems 36 (2023): 53728-53741. aka DPO
[6]. Schulman, John, Philipp Moritz, Sergey Levine, Michael Jordan, and Pieter Abbeel. "High-dimensional continuous control using generalized advantage estimation." arXiv preprint arXiv:1506.02438 (2015). aka GAE
[7]. Sutton, Richard S., and Andrew G. Barto. "Reinforcement learning: An introduction second edition." Adaptive computation and machine learning: The MIT Press, Cambridge, MA and London (2018). 按照强化学习的术语习惯,每一个完整的采样回答也称之为幕(episode),或者也可以称之为一个轨迹。↩︎