这个系列主要是对深度学习中常见的各种层的反向求导细节进行学习和介绍，并且辅以代码予以理解，本章介绍的是卷积层，考虑到不同通道之间的转换并且不同的stride，padding等，卷积层的反向求导研究起来也是颇有意思的。如有谬误请联系指出，谢谢。

我们经常会谈到“业务”一词，作为在互联网圈混的我们，也经常会听到“技术赋能业务”这一概念。笔者作为刚毕业时间不满一年的职场新人，在学校（包括在实习的时候，见[1]）时期接触最多的是技术相关的内容，对“业务”这一概念其实没有太多的认识，对于技术如何给业务“赋能”更是完全没有头绪。笔者从实习开始到工作到现在也接近一年多时间了，在此尝试去理解什么是业务，以及技术如何支持业务，赋能业务。

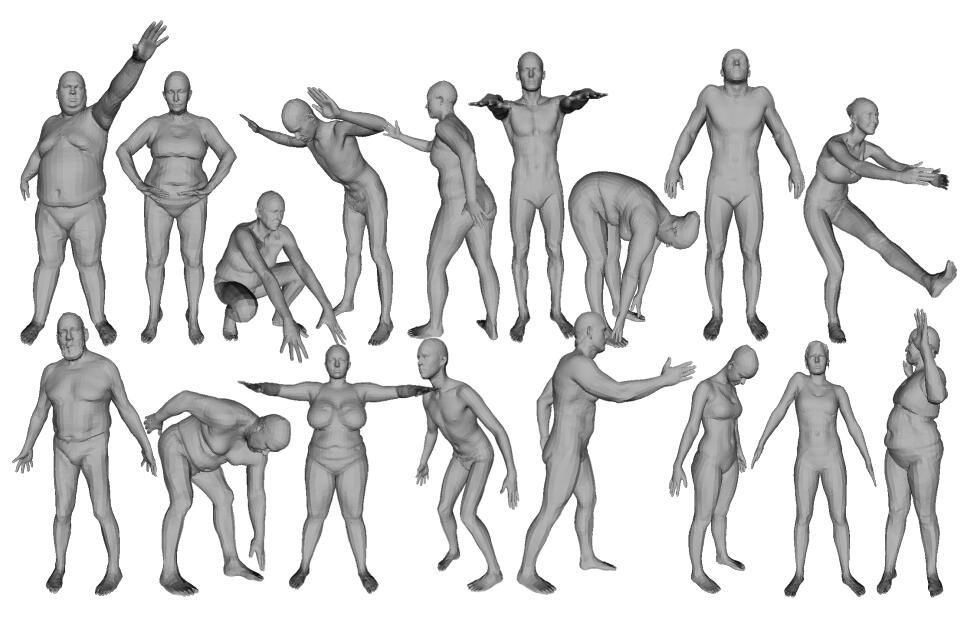
笔者最近在做和motion capture动作捕捉相关的项目，学习了一些关于人体3D mesh模型的知识，其中以SMPL模型最为常见，笔者特在此进行笔记，希望对大家有帮助，如有谬误，请在评论区或者联系笔者指出，转载请注明出处，谢谢。

近期在看Shift-GCN的论文[1]，该网络是基于Shift卷积算子[2]在图结构数据上的延伸。在阅读源代码[3]的时候发现了其对于Non-Local Spatial Shift Graph Convolution有意思的实现方法，在这里简要记录一下。

本文翻译自《Up-sampling with Transposed Convolution》，这篇文章对转置卷积和反卷积有着很好的解释，这里将其翻译为中文，以飨国人。

笔者在前文 [1] 中曾经介绍过一种大规模图文匹配模型BriVL，该模型基于海量数据进行对比学习预训练，从而可以实现很强的多模态建模能力。WenLan 2.0是该工作的后续探索，本文尝试简单对其进行笔记。

之前我们在[1]中介绍过超大负样本对于对比学习训练的重要意义，并且在[2,3]中介绍了MoCo，Memory Bank等方法去突破硬件限制地去进一步增大负样本数量。然而，之前这些方法都尝试在单模态数据上进行对比学习[4]，在文章[5]中，作者团队提出了WenLan项目，尝试在多模态模型中采用MoCo的形式进行大尺度负样本对比学习。

文章[1]的作者发现在多模态分类模型中，经常出现最好的单模态模型比多模态模型效果还好的情况，作者认为这是由于多模态模型的容量更大，因此更容易过拟合，并且由于不同模态的信息过拟合和泛化有着不同的节奏，如果用同一个优化策略进行优化，那么很可能得到的不是一个最佳的结果。也就是说作者认为目前的多模态融合方式还不是最合适的，因此在[1]中提出了一种基于多模态梯度混合的优化方式...

CLIP是近年来在多模态方面的经典之作，其用大量的数据和算力对模型进行预训练，使得模型的zero-shot性能甚至可以匹敌众多数据集上的监督SOTA，实在让人惊叹不已，本文简要纪录下笔者阅读该文后的读后感以及一些启发。

【论文极速看】CLIP-Lite：一种不依赖于负样本数量的高效多模态学习方法